Question

 

2.    На стороне АС треугольника ABC с площадью 36 см2 взята точка D, AD : DC =1:5. Найдите площадь треугольника ABD.

 

Answer 1

Площадь треугольника равна половине произведения высоты на сторону, к которой  проведена. 

S=a•h:2

• Если высоты двух треугольников равны, то их площади относятся как основания.

Высота ∆ ADC и ∆ ABC общая. 

Подробно.

S(ABD):S(ABC)=AD:AC

Точка D по условию делит АС в отношении 1:5. 

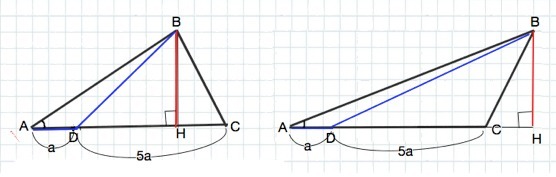
Примем AD=a, тогда DC=5a. 

AC=а+5а=6a 

S(ABD):A(ABC)=1/6

S(ABC)=36

S(ABD)=36:6=6 см²

-----------

Площадь треугольника можно найти и по формуле 

S=a•b•sinα:2,  где a и b стороны треугольника, α - угол между ними. 

Угол А общий для ∆ABD и ∆ABC, поэтому 

S (ABD):S (ABC)=AB•AD:AB•AC, т.е. получается то же отношение AD:AC, равное для данного треугольника 1/6.