Предмет: Алгебра,
автор: Katin
помогите пожалуйста сделать номер 17.29 б,в,г и 17.31 полностью плииииз(11 класс
Приложения:
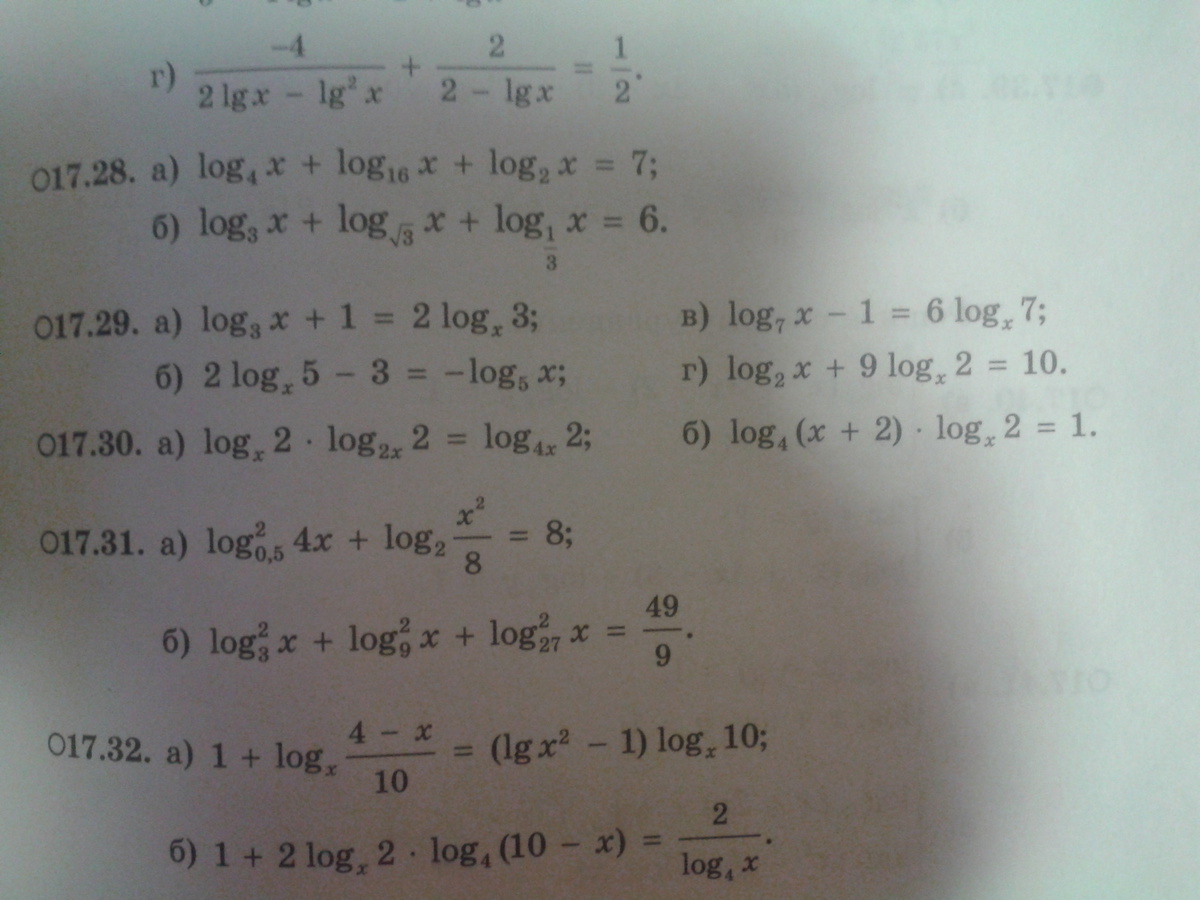
Ответы
Автор ответа:
0
решение смотри на фотографии
Приложения:

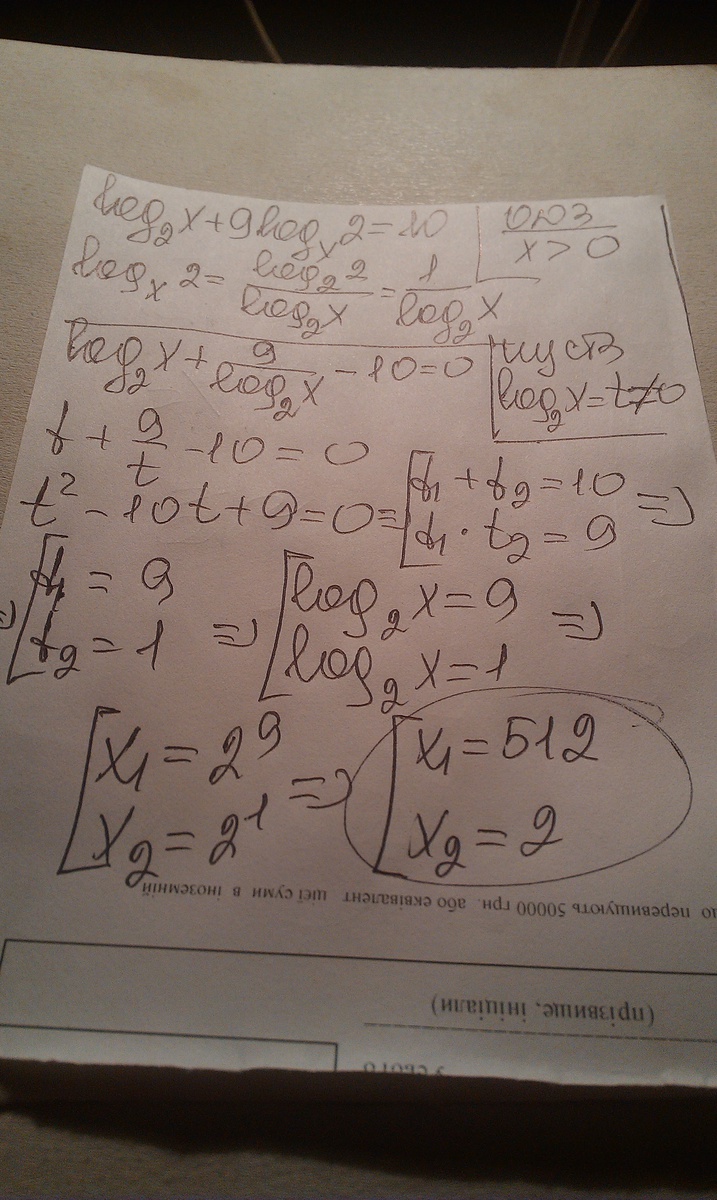
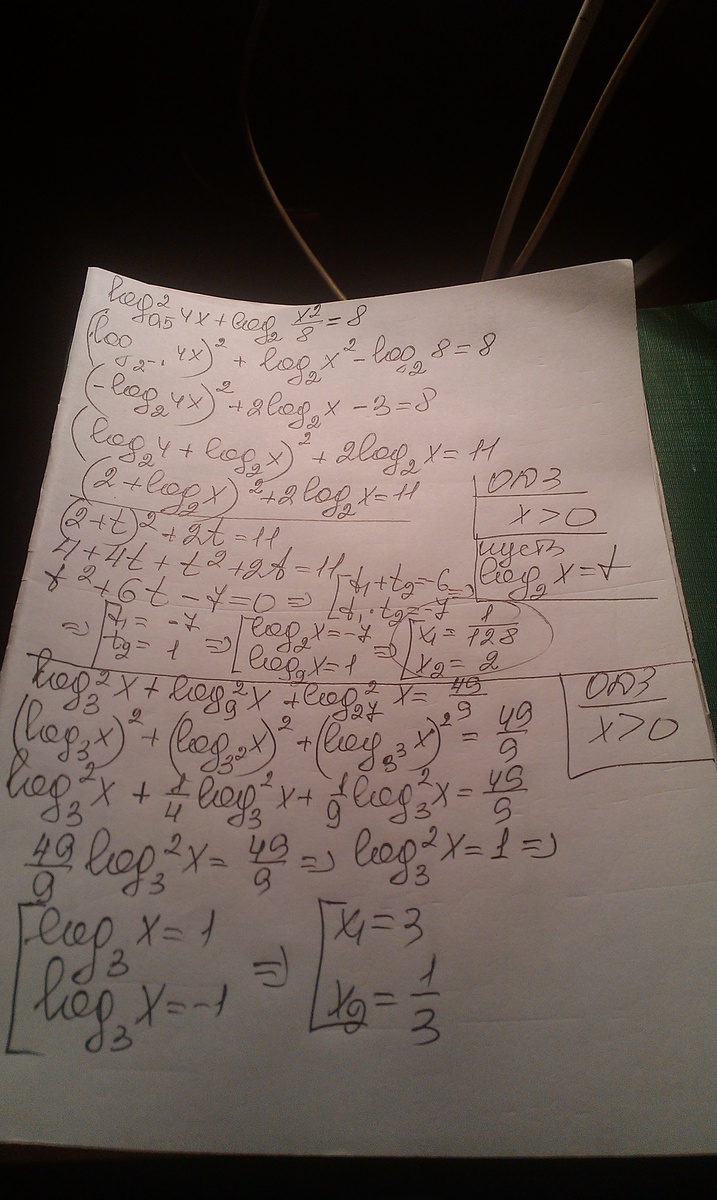
Автор ответа:
0
17.29
Все уравнения однотипные.ОДЗ: х>0, x≠1
Применяем формулу перехода к другому основанию:
б)
Замена переменной:

тогда

Уравнение принимает вид:


t≠0
2t²-3t+1=0
D=9-8=1
t=(3-1)/4=1/2 или t=(3+1)/4=1
Возвращаемся к переменной х

х=5
или

√x=5
x=25
Ответ. 5; 25
в)Замена переменной:

тогда

Уравнение принимает вид:


t≠0
6t²+t-1=0
D=1-4·6·(-1)=1+24=25
t=(-1-5)/12=-1/2 или t=(-1+5)/12=1/3
Возвращаемся к переменной х

1/√x=7 ⇒ x=1/49
или

∛x=7
x=343
Ответ. 1/49; 343
г)Замена переменной:

тогда

Уравнение принимает вид:


t≠0
9t²-10t+1=0
D=100-4·9·=64
t=(10-8)/18=1/9 или t=(10+8)/18=1
Возвращаемся к переменной х

![sqrt[9]{x}=2, \ x=2 ^{9} \ x=512 sqrt[9]{x}=2, \ x=2 ^{9} \ x=512](https://tex.z-dn.net/?f=+sqrt%5B9%5D%7Bx%7D%3D2%2C+%5C+x%3D2+%5E%7B9%7D+%5C+x%3D512++) или
или
x=2
Ответ. 2; 512
17.31


Уравнение примет вид:

Замена переменной:
Применяем формулу перехода к другому основанию:


t²-6t-7=0
D=(-6)²-4·(-7)=36+28=64
t=(6-8)/2=-1 или t=(6+8)/2=7
Возвращаемся к переменной х:

х=2

х=1/128
Ответ. 2; 1/128.
б)
Уравнение примет вид:

Умножим на 36:



Все уравнения однотипные.ОДЗ: х>0, x≠1
Применяем формулу перехода к другому основанию:
б)
Замена переменной:
тогда
Уравнение принимает вид:
t≠0
2t²-3t+1=0
D=9-8=1
t=(3-1)/4=1/2 или t=(3+1)/4=1
Возвращаемся к переменной х
х=5
или
√x=5
x=25
Ответ. 5; 25
в)Замена переменной:
тогда
Уравнение принимает вид:
t≠0
6t²+t-1=0
D=1-4·6·(-1)=1+24=25
t=(-1-5)/12=-1/2 или t=(-1+5)/12=1/3
Возвращаемся к переменной х
1/√x=7 ⇒ x=1/49
или
∛x=7
x=343
Ответ. 1/49; 343
г)Замена переменной:
тогда
Уравнение принимает вид:
t≠0
9t²-10t+1=0
D=100-4·9·=64
t=(10-8)/18=1/9 или t=(10+8)/18=1
Возвращаемся к переменной х
x=2
Ответ. 2; 512
17.31
Уравнение примет вид:
Замена переменной:
Применяем формулу перехода к другому основанию:
t²-6t-7=0
D=(-6)²-4·(-7)=36+28=64
t=(6-8)/2=-1 или t=(6+8)/2=7
Возвращаемся к переменной х:
х=2
х=1/128
Ответ. 2; 1/128.
б)
Уравнение примет вид:
Умножим на 36:
Приложения:

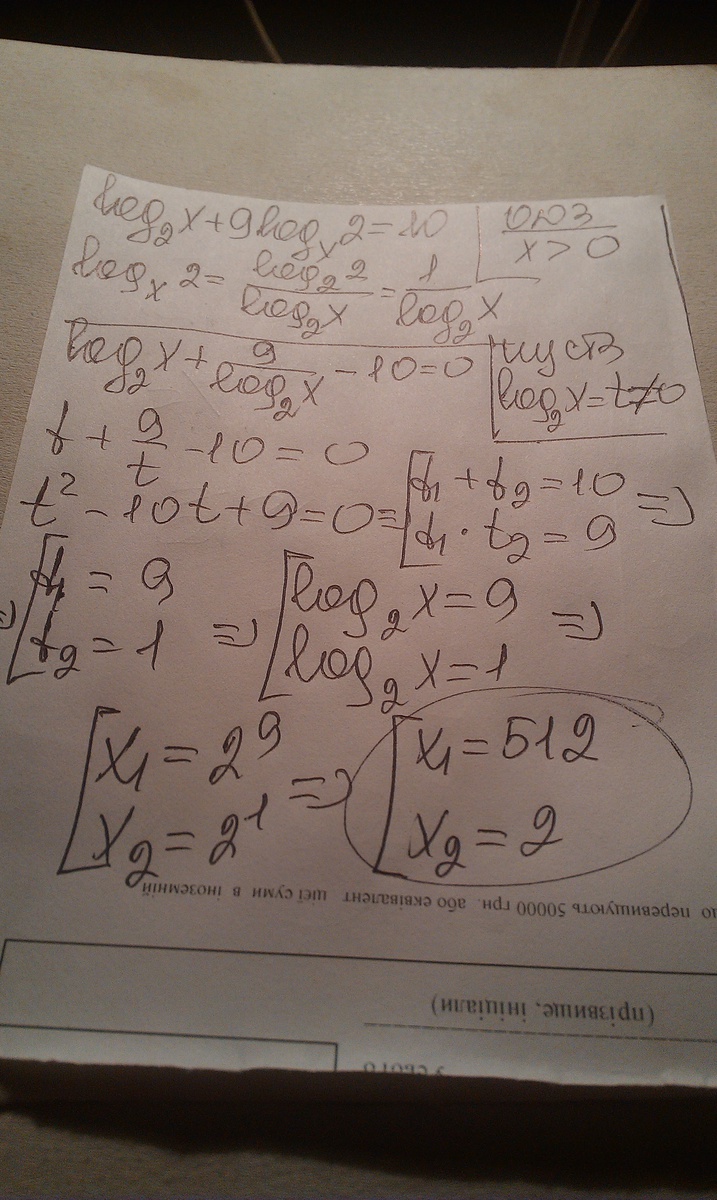
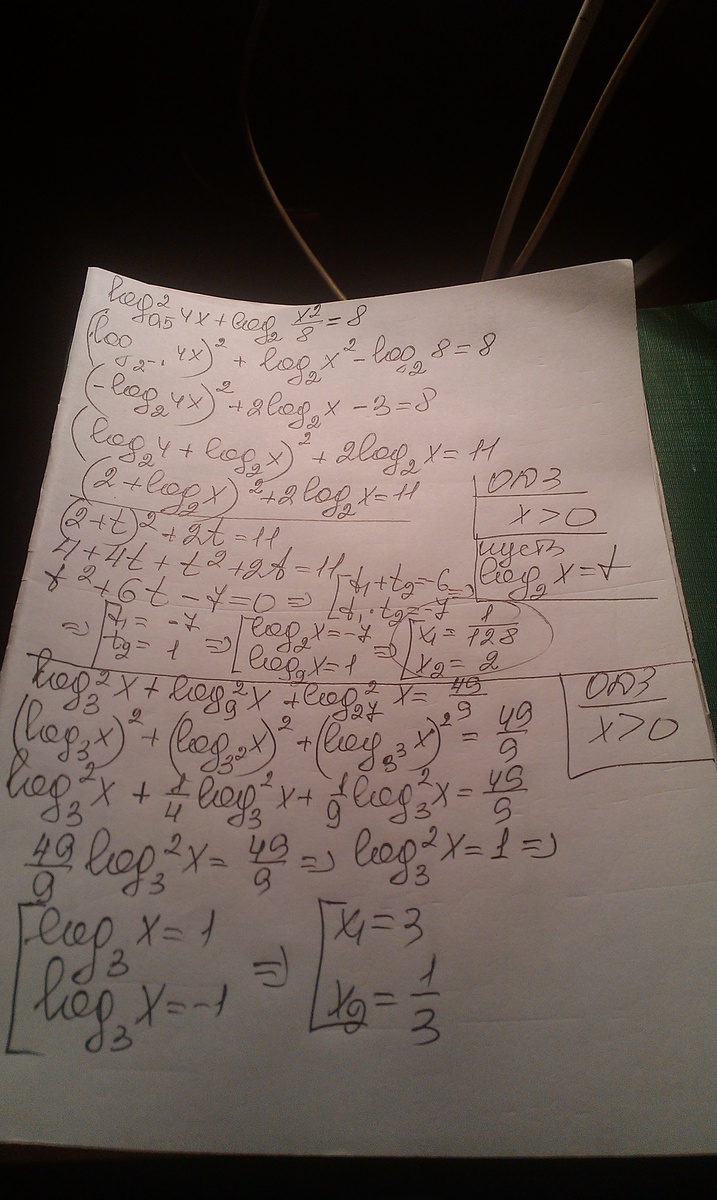
Автор ответа:
0
спасибо большое)
Автор ответа:
0
Больше не буду решать сразу несколько уравнений в одном вопросе. Делите на несколько частей. Устала редактировать решение
Автор ответа:
0
log_{3}x=2 или log_3x=-2 Ответ. 9; 1/9
Автор ответа:
0
а если будет 499+499б ?))))
Автор ответа:
0
буду ставить нарушение. По правилам Сервиса не более трех задач в вопросе. А здесь 6 и решение не умещается. Когда последние строчки пишешь, то весь текст автоматически форматируется и превращается в сплошной набор букв,без абзацев и строчек. Приходится заново править. Одно неловкое движение - и все начинается сначала
Похожие вопросы
Предмет: Английский язык,
автор: aidajumabaeva483
Предмет: Другие предметы,
автор: derteri2015
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: zxcvbnm9
Предмет: География,
автор: d1asha123456789