Предмет: Алгебра,
автор: machete998
Помогите пожалуйста с решением, никак понять не могу
Приложения:
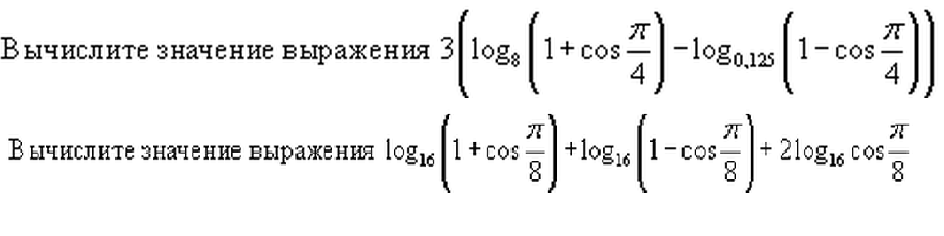
Ответы
Автор ответа:
0
Автор ответа:
0
спасибо большое
Похожие вопросы
Предмет: Химия,
автор: kesanela1
Предмет: Информатика,
автор: milana0016377355
Предмет: Биология,
автор: dierbekmail78
Предмет: Математика,
автор: polosatik95
Предмет: Математика,
автор: 45467