Предмет: Алгебра,
автор: наНана
Помогите пожалуйста!
Приложения:
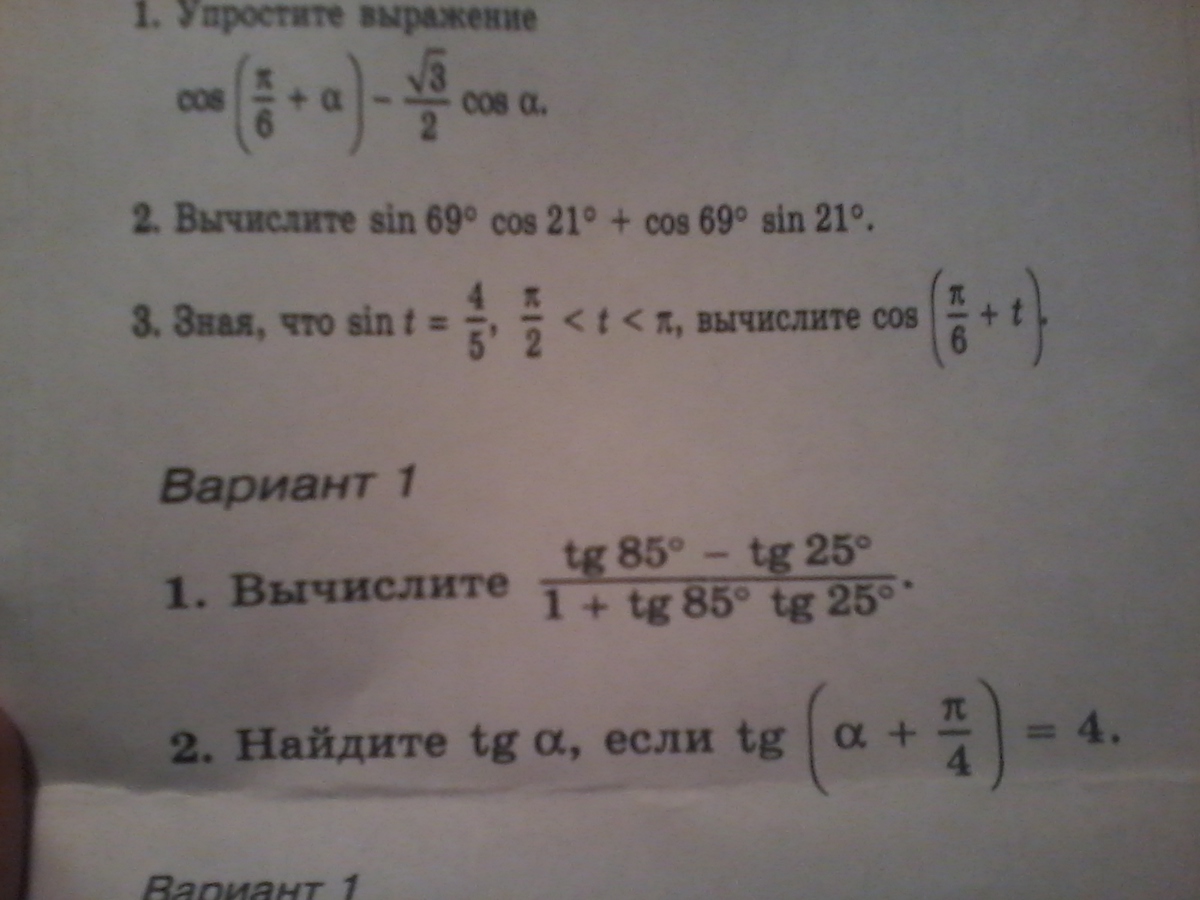
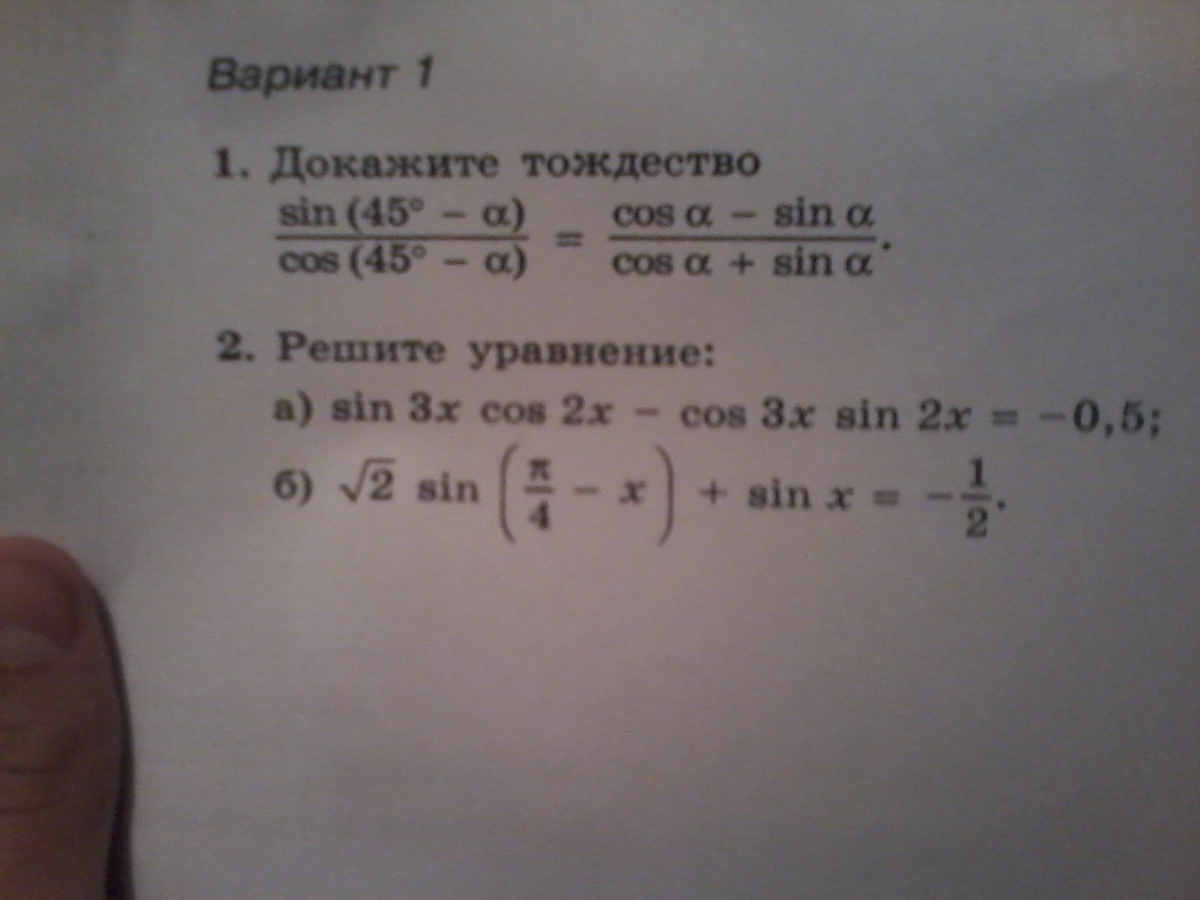
Ответы
Автор ответа:
0
1)cos(π/6+a)-√3/2cosa=cosπ/6cosa+sinπ/6sina-cosπ/6cosa=1/2*sina
2)sin69cos21+cos69sin21=sin(69+21)=sin90=1
3)sint=4/5
cost=-√1-16/25=-√9/25=-3/5
cos(π/6+t)=cosπ/6cost-sinπ/6sint=√3/2*(-3/5)-1/2*4/5=-3√3/10-4/10=-(3√3+4)/10
1)(tg85-tg25)/(1+tg85tg25)=tg(85-25)=tg60=√3
2)tg(a+π/4)=(tga+tgπ/4)/(1-tgatgπ/4)=(tga+1)/(1-tga)=4
tga+1=4-4tga
tga+4tga=4-1
5tga=3
tga=0,6
1)sin(45-a)/cos(45-a)=(sin45cosa-cos45sina)/(cos45cosa+sin45sina)=
=(√2/2cosa-√2/2sina)/(√2/2cosa+√2/2sina)=√2/2(cosa-sina)/√2/2(cosa+sina)=
=(cosa-sina)/(cosa+sina)
2)sin3xcos2x-cos3xsin2x=-0,5
sin(3x-2x)=-0,5
sinx=-0,5
x=(-1)^n+1*π/6+πn
√2sin(π/4-x)+sinx=-1/2
√2sinπ/4cosx-√2cosπ/4sinx+sinx=-1/2
√2*1/√2cosx-√*1/√2sinx+sinx=-1/2
cosx-sinx+sinx=-1/2
cosx=-1/2
x=+-2π/3+2πn
2)sin69cos21+cos69sin21=sin(69+21)=sin90=1
3)sint=4/5
cost=-√1-16/25=-√9/25=-3/5
cos(π/6+t)=cosπ/6cost-sinπ/6sint=√3/2*(-3/5)-1/2*4/5=-3√3/10-4/10=-(3√3+4)/10
1)(tg85-tg25)/(1+tg85tg25)=tg(85-25)=tg60=√3
2)tg(a+π/4)=(tga+tgπ/4)/(1-tgatgπ/4)=(tga+1)/(1-tga)=4
tga+1=4-4tga
tga+4tga=4-1
5tga=3
tga=0,6
1)sin(45-a)/cos(45-a)=(sin45cosa-cos45sina)/(cos45cosa+sin45sina)=
=(√2/2cosa-√2/2sina)/(√2/2cosa+√2/2sina)=√2/2(cosa-sina)/√2/2(cosa+sina)=
=(cosa-sina)/(cosa+sina)
2)sin3xcos2x-cos3xsin2x=-0,5
sin(3x-2x)=-0,5
sinx=-0,5
x=(-1)^n+1*π/6+πn
√2sin(π/4-x)+sinx=-1/2
√2sinπ/4cosx-√2cosπ/4sinx+sinx=-1/2
√2*1/√2cosx-√*1/√2sinx+sinx=-1/2
cosx-sinx+sinx=-1/2
cosx=-1/2
x=+-2π/3+2πn
Похожие вопросы
Предмет: Математика,
автор: angelokb1089
Предмет: Математика,
автор: nurajymturlbaeva
Предмет: Литература,
автор: pozitifcreatif
Предмет: Математика,
автор: svetlanakolom
Предмет: Математика,
автор: Dok20344