Предмет: Математика,
автор: Aissulu
Найдите интеграл номер 8,5,23
Приложения:
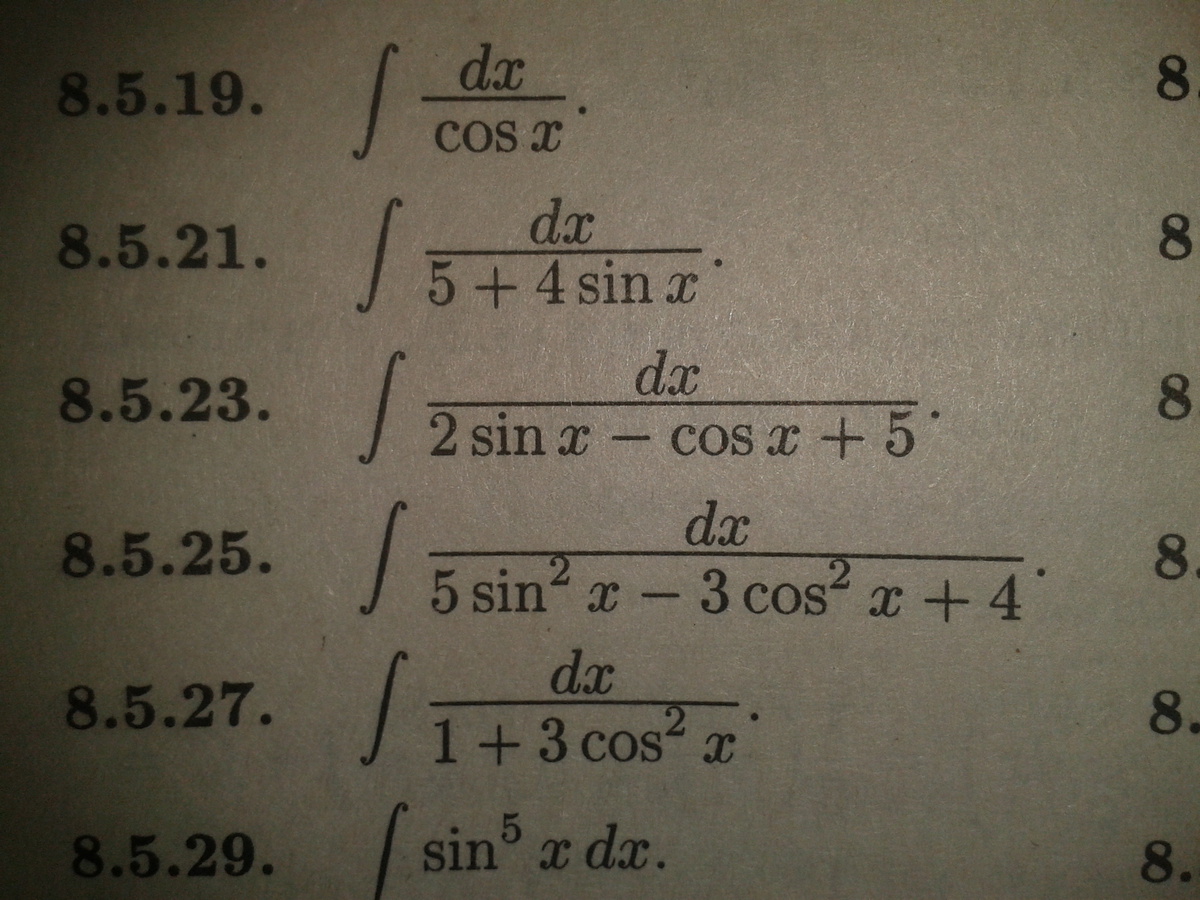
Ответы
Автор ответа:
0
Замена переменной

Тогда

Подынтегральная дробь примет вид:

Выделим полный квадрат в знаменателе:

Итак,

Тогда
Подынтегральная дробь примет вид:
Выделим полный квадрат в знаменателе:
Итак,
Автор ответа:
0
вполне возможно. Напишите какой
Автор ответа:
0
http://znanija.com/task/9164920
Автор ответа:
0
вы найдете ошибку у себе в решении иди это в учебнике опечатка?
Автор ответа:
0
я думаю, что в учебнике, потому как корня из пяти не получить. Можно взять производную и проверить оба ответа. Попробую
Автор ответа:
0
хорошо
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: kdjkodfj
Предмет: Физкультура и спорт,
автор: vk900789
Предмет: История,
автор: РиткОНовикОва
Предмет: Литература,
автор: Katya0765787568757