Question

При каких значениях 'a' уравнение x(x+3)²+a=0. имеет 3 корня.

Answer 1

Попробуем нарисовать  примерный эскиз графика.
y=x*(x+3)^2=x^3+6*x^2+9x
Понятно  что  y(0)=0 ,а при возрастании x начиная от 0, функция растет.
При  x<0 все  чуточку сложнее.
Найдем производную функции:
y'=3*x^2+12*x+9=0
Найдем точки  подозреваемые  на  экстремум:
3*x^2+12*x+9=0
x^2+4x+3=0
x1=-1
x2=-3
y'=3*(x+1)*(x+3)
Найдем знаки  производной на промежутках: 
Очевидно: y(0)=9>0 ,откуда очевидна  расстановка  знаков.
(Рисунок 1)  
Откуда очевидно  что  x=-1  -точка минимума , y(-1)=-4
x=-3 -точка максимума,  y(-3)=0.
При  x<-3  при  уменьшении  далее аргумента  функция очевидно  убывает.
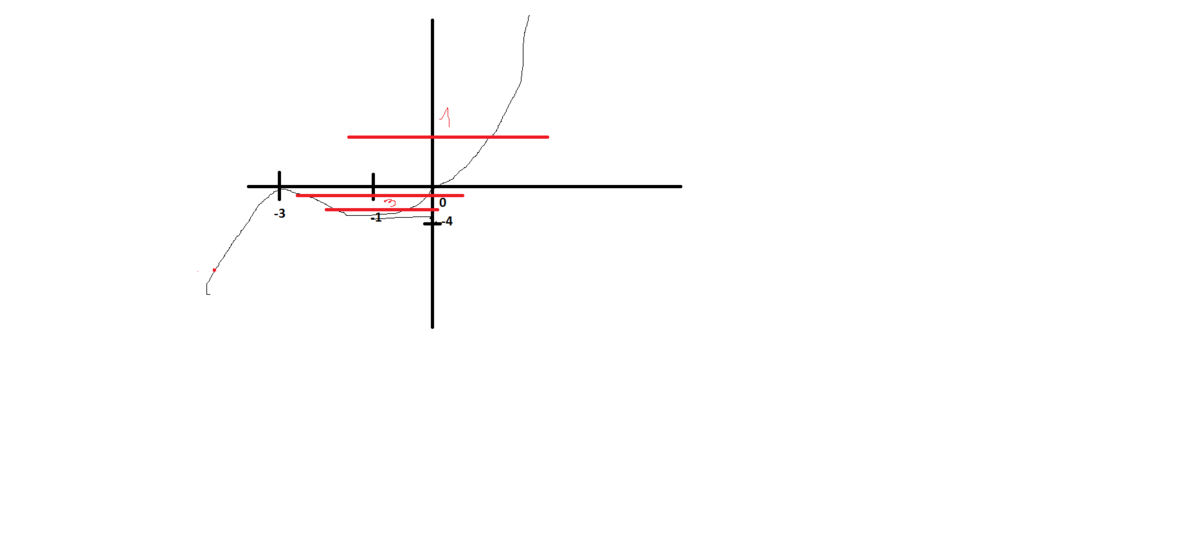
Откуда  можно начертить эскиз графика. (Рисунок 2)
Наше  уравнение:
x*(x+3)^2=-a
Имеет  3 корня  когда прямая y=-a имеет  3 точки  пересечения с графиком.
Из  рисунка видно  что это те -a,что -a∈(0;-4)
Или a∈(0;4)
Ответ:a∈(0;4) ( В  критичных точкаx a=4  a=0 по  2 решения,
Во всех  остальных по  одному решению)