Предмет: Геометрия,
автор: zaki
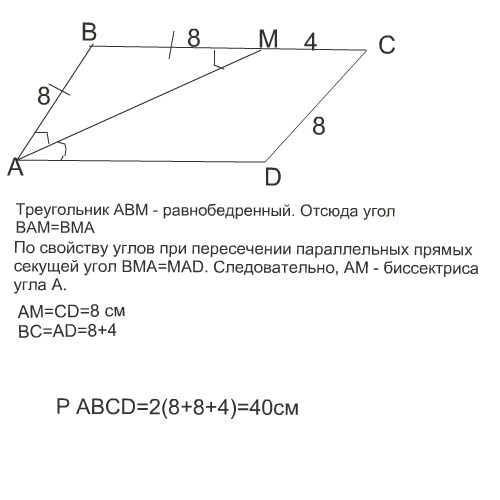
На стороне BC параллелограмма ABCD взята точка m так,что AB=BM
1)доказать что АМ - бессиктриса углов BAD
2)найти периметр параллелограмма если CD - 8см CM - 4 см
Ответы
Автор ответа:
0
АМ отсекает от параллелограмма равнобедренный треугольник АВМ ( по условию задачи АВ=ВМ). Поэтому углы ВАМ и ВМА равны при основании АМ этого треугольника.
Но по свойству углов при параллельных прямых и секущей угол ВМА равен углу МАD. Отсюда угол А разделен отрезком АМ на два равных угла. АМ - биссектриса угла А.
---------------------------
Сторона АВ=CD=8см
АD=ВС=8+4=12 см
Периметр параллелограмма
Р=2(8+12)=40 см
Приложения:
Похожие вопросы