Question

Верно ли утверждение, что если прямая не лежащая в плоскости, параллельна ей, то она параллельна любой прямой, лежащей в этой плоскости.
Почему?

Answer 1

Ответ:

Верно.

Объяснение:

Это признак параллельности прямой и плоскости:

Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в плоскости, то она параллельна и самой плоскости.

Доказательство:

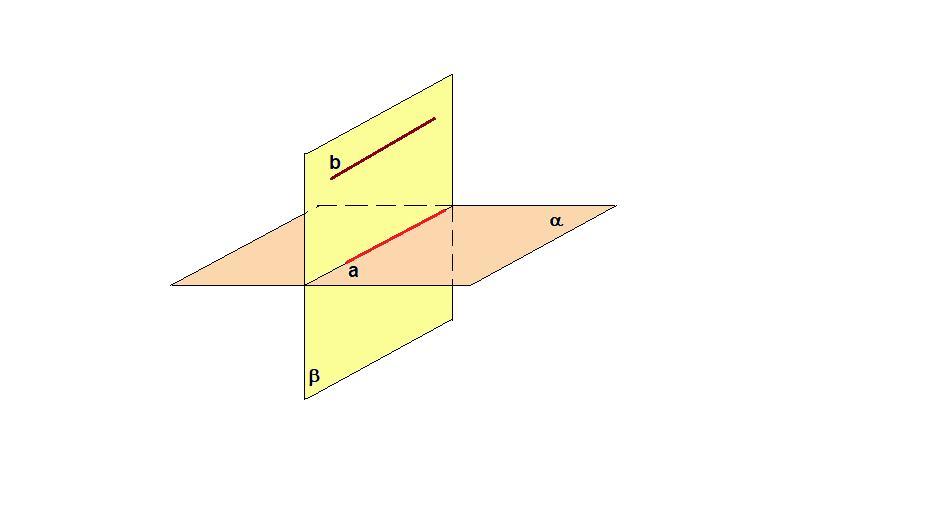
Пусть прямая b параллельна прямой а, лежащей в плоскости α. Докажем, что прямая b параллельна плоскости α.

Через две параллельные прямые можно провести единственную плоскость. Проведем плоскость β через прямые а и b.

Так как прямая а лежит в двух плоскостях, то она является линией пересечения плоскостей.

Предположим, что прямая b не параллельна плоскости α, т.е. пересекает ее. Тогда точка пересечения лежит на прямой а (на линии пересечения плоскостей), но тогда b пересекает прямую а, а это противоречит условию.

Значит b║α. Что и требовалось доказать.