Question

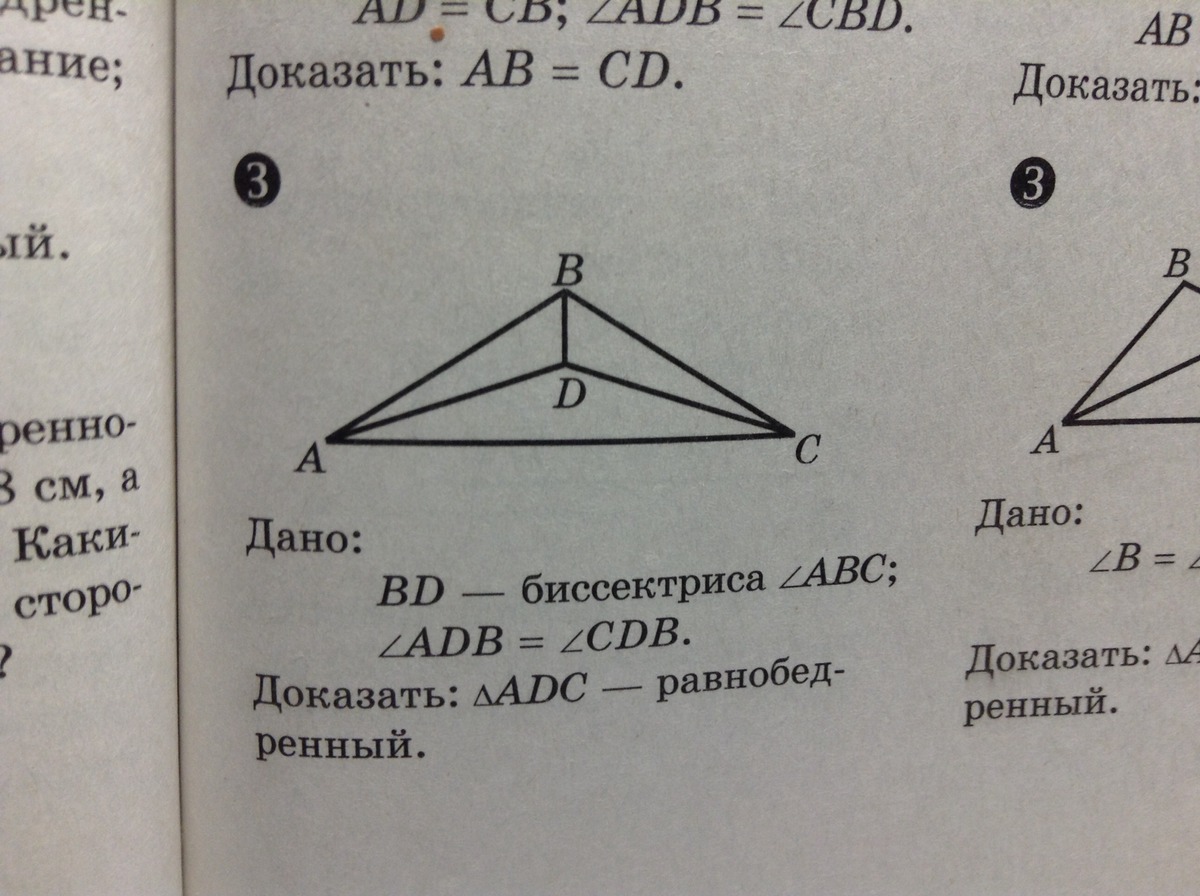
Помогите решить пожалуйста! Дано: BD-биссектриса /_ ABC; /_ ADB=/_ CDB
Доказать: ^ADC- равнобедренный

Answer 1

Рассмотрим ΔADB и ΔCDB.
BD - общая сторона
уголADB = уголCDB (по условию)
уголABD = уголCBD (т.к. BD-биссектриса углаABC)
Значит ΔADB = ΔCDB по 2-ому признаку равенства Δ. 
Из равенства Δ следует, что
AD=DC.
Следовательно  ΔADC - равнобедренный.

Answer 2

спасибо)))))