Предмет: Алгебра,
автор: Леннон
Помогите пожалуйста решить
подробно все распишите
Приложения:

Ответы
Автор ответа:
0
Перепишем второе неравенство:

или

или
(х²+у-1)(х²+у+1)<0
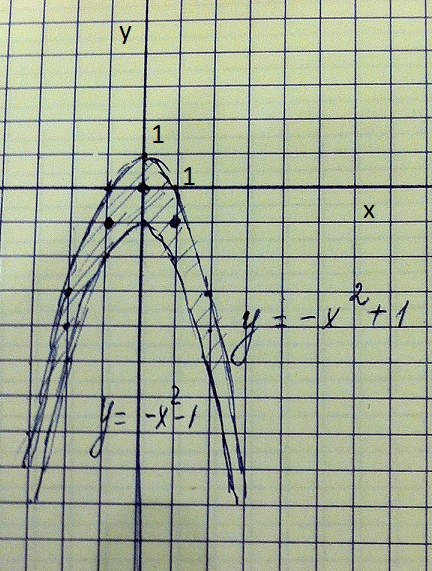
Геометрическое место точек, заданных данным неравенством, это точки между двумя параболами
у=-х²+1 и у=-х²-1
(см. рисунок)
Точки с целочисленными координатами лежат на параболе у=-х²
(0;0) (-1;-1); (1;1) (2;-4) (-2;-4)
ОДЗ первого неравенства: 3х+2≥0 ⇒ х≥-2/3
Проверим удовлетворяет ли каждая точка (0;0)
первому неравенству:
х=0
3√(3·0+2)<1+√2+√5
3√2-√2<1+√5
2√2<1+√5
Возводим обе части неравенства в квадрат
8<1+2√5+5
8<6+2√5
2<2√5
1<√5- верно
х=1
3√(3·1+2)<1+√2+√5
3√5-√5<1+√2
2√5<1+√2
Возводим обе части неравенства в квадрат
20<1+2√2+2
17<2√2-неверно
х=2
3√(3·2+2)<1+√2+√5
3√8<1+√2+√5
3·2√2<1+√2+√5
5√2<1+√5- неверно
Ответ. (0;0)
или
или
(х²+у-1)(х²+у+1)<0
Геометрическое место точек, заданных данным неравенством, это точки между двумя параболами
у=-х²+1 и у=-х²-1
(см. рисунок)
Точки с целочисленными координатами лежат на параболе у=-х²
(0;0) (-1;-1); (1;1) (2;-4) (-2;-4)
ОДЗ первого неравенства: 3х+2≥0 ⇒ х≥-2/3
Проверим удовлетворяет ли каждая точка (0;0)
первому неравенству:
х=0
3√(3·0+2)<1+√2+√5
3√2-√2<1+√5
2√2<1+√5
Возводим обе части неравенства в квадрат
8<1+2√5+5
8<6+2√5
2<2√5
1<√5- верно
х=1
3√(3·1+2)<1+√2+√5
3√5-√5<1+√2
2√5<1+√2
Возводим обе части неравенства в квадрат
20<1+2√2+2
17<2√2-неверно
х=2
3√(3·2+2)<1+√2+√5
3√8<1+√2+√5
3·2√2<1+√2+√5
5√2<1+√5- неверно
Ответ. (0;0)
Приложения:
Автор ответа:
0
Огромное спасииибище!
Автор ответа:
0
Не совсем, конечно, обосновано, почему дальше- больше. И почему остальные точки с абсциссами больше чем 1 и 2 не подойдут.
Автор ответа:
0
А вы не знаете способы другие решения таких систем?
как вообще подобное решать - находить целые значения?
как вообще подобное решать - находить целые значения?
Автор ответа:
0
как понять что нужно делать, чтобы найти эти целые значения? вы как рассуждаете? первые мысли при решении такого задания?
Похожие вопросы
Предмет: Другие предметы,
автор: ki066792
Предмет: Математика,
автор: safurasobirzanova
Предмет: Алгебра,
автор: darakovatkina
Предмет: Биология,
автор: madeinsiberia
Предмет: Математика,
автор: Аноним