Question

помогите даю 25 пунктов

Answer 1

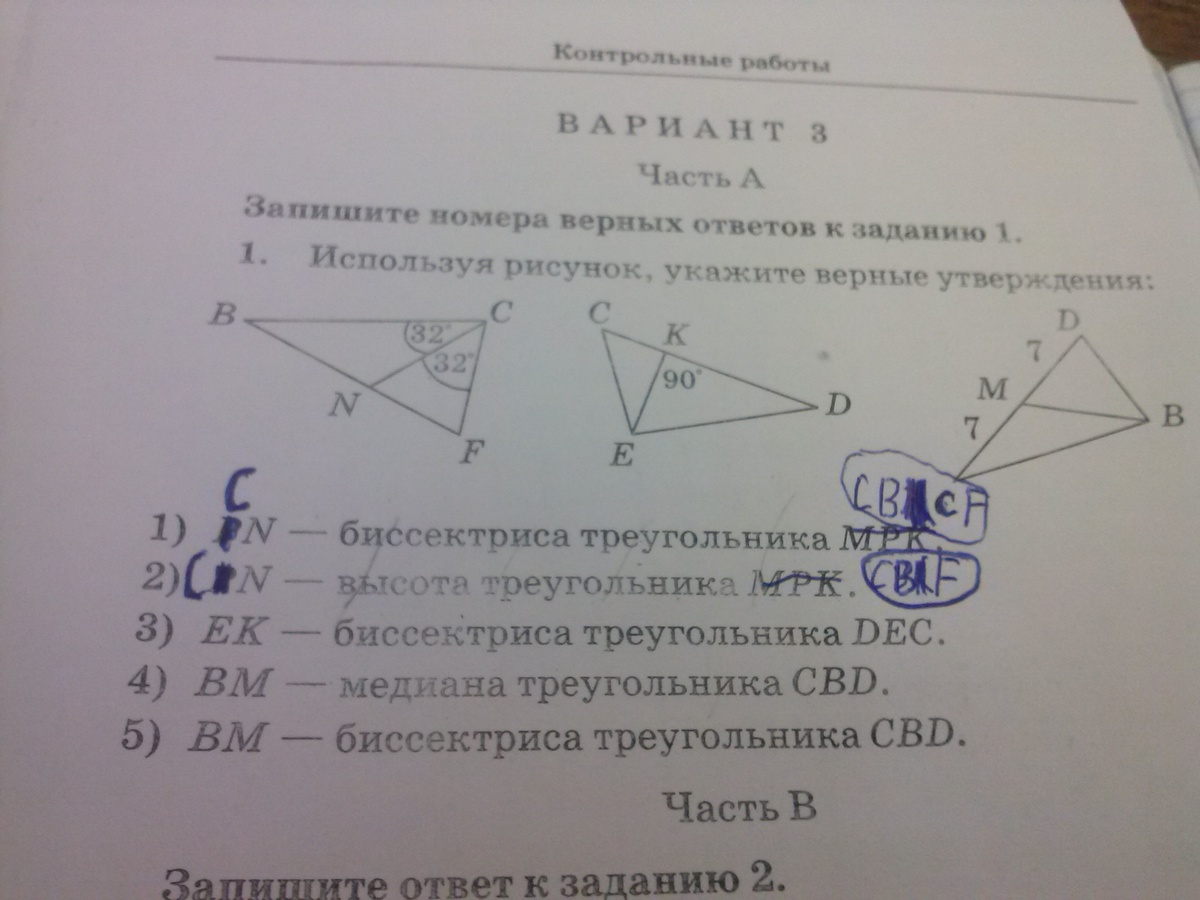
Часть А
1) CN- биссектриса ΔCBF
4) BM - медиана ΔCBD

Часть С
3. DK=KB (по условию)
    KC - общая
    угол DKC = угол CKB (т.к. KC-биссектриса угла DKB)
    ΔKDC=ΔKBC по 1 признаку равенства треугольников.
4. Рассмотрим ΔNBA и ΔKBC.
   NB=KB (по св-ву равнобедренного Δ)
   NA=KC (по условию)
   уголBNA= уголBKC (по св-ву равнобедренного Δ)
   ΔNBA = ΔKBC (по 1 признаку равенства Δ)
   Отсюда уголNBA= уголKBC
5*. Рассмотри ΔBAM и ΔDAM.
     BM=DM (по условию)
     AM - общая
     уголBMA = уголAMD=90 град
     ΔBAM=ΔDAM (по 1 признаку равенства Δ)
     Из равенства Δ следует, что
     уголBAM= уголDAM=35 град
     уголBAD=уголBAM + уголDAM=35 град +35 град=70 град

Часть В.
2. уголORP=угол2=42 град (вертикальные углы)
    Так как ΔPOR - равнобедренный, то
    угол1=уголORP=42 град
   Ответ: 42 град

Answer 2

1) : верные : 1 , 3 , 4 .
2) : Угол 2 - внешний . Угол OPR = 42 градуса (он вертикален углу 2) . А если данный треугольник равнобедренный , как сказано в задаче , то его при основе PR равны и угол 1 = 42 градуса .
3) : Если луч КС бисектриса угла DKB , то угол DКС равен углу СКВ , а КВ = DK , то треугольник СКВ равен треугольнику DКС по теореме о равенстве треугольников , если по одной из их сторон равны и по одному из их углов равны .
4) : NA = KC и если данный треугольник равнобедренный , то его стороны NB и KB равны . Поетому треугольники NBA и KBC равны по теореме о равенстве треугольников .если по две их стороны равны . А если эти треугольники равны , то углы NBA и KBC равны .
5) : Диаметр АС делит хорду ВD пополам ,а дополнительныно нарисованые хорды ВА и DА имеют общий конец в точке А , и поэтому равны (аналогично углы , которые они образуют (ВАС и DАС) равны). Угол ВАС равен 35 градусам и поэтому угол ВАD равен их сумме , 35 + 35 = 70 .