Предмет: Геометрия,
автор: LanaBelka
Найдите на оси у точку, равноудалённую от точек А(-3; 7; 4) и В(2; -5; -1)
Помогите, пожалуйста :)
Приложения:
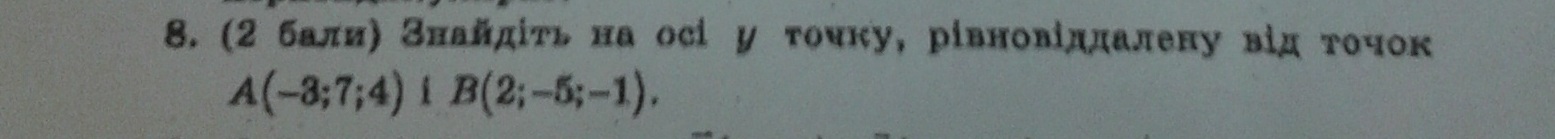
Ответы
Автор ответа:
0
А(-3; 7; 4)
В(2; -5; -1)
Точка С лежит на оси ОУ, значит С(0;у;0) и |AC|=|BC|
Вектор АС(0-(-3);у-7;0-4)=(3;у-7;-4)
|AC|=
Вектор ВС(0-2;у+5;0-(-1))=(-2;у+5;1)
|DC|=
|AC|=|BC|
C(0; 1 5/6; 0)
Автор ответа:
0
если мы ищем на оси точку, то значит две другие координаты будут равны 0.
С(0;y;0)
|AC| = |BC|
если равны корни, то и равны подкоренные выражения:
[tex]y=frac{44}{24}[tex]
Похожие вопросы
Предмет: Алгебра,
автор: danchik2007yt
Предмет: Информатика,
автор: sharovari
Предмет: Математика,
автор: mrreedle93
Предмет: Математика,
автор: DjaGer