Центр описанной около треугольника окружности симметричен центру вписанной в него окружности относительно одной из сторон.Найдите углы треугольника.
ОТМЕЧУ КАК ЛУЧШЕЕ РЕШЕНИЕ
Ответы
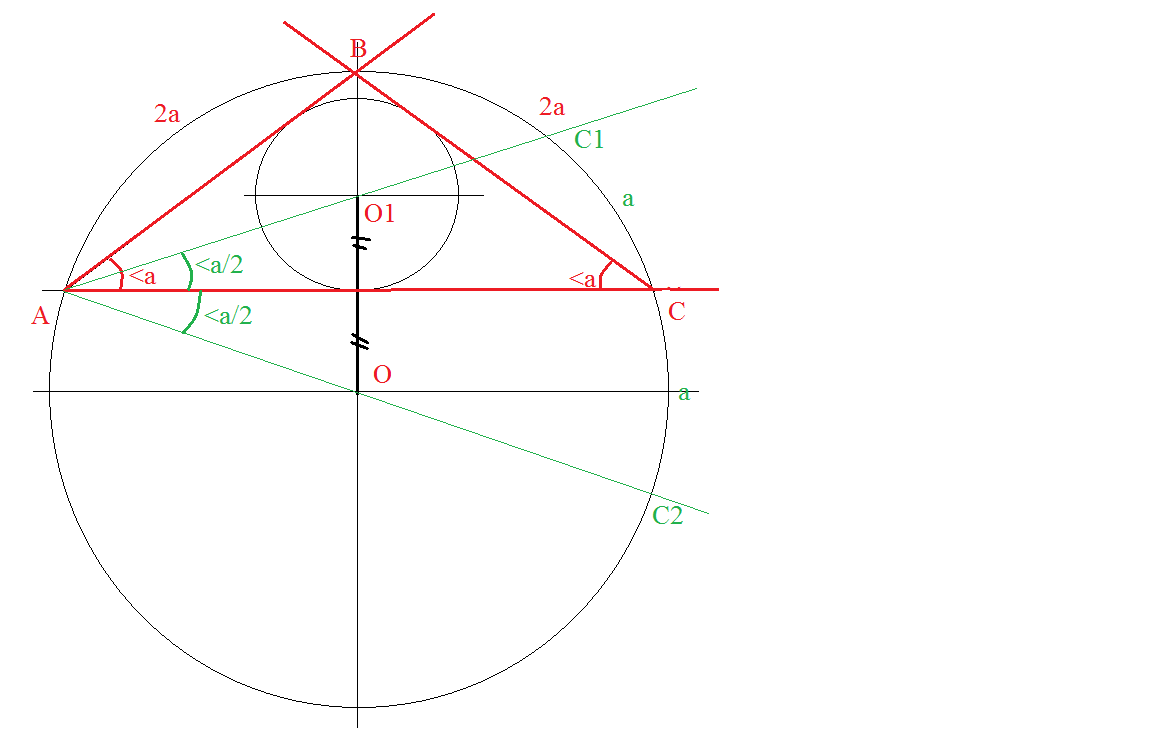
сделаем построение по условию
центры окружностей O и О1 -симметричны относительно стороны АС
значит (ОО1) перпендикулярна (АС)
треугольник АВС - равнобедренный |AB| = |BC| -иначе не будет выполняться условие симметричности ЦЕНТРОВ окружностей
обозначим <BAC=<BCA=<a - это вписанные углы
По теореме о вписанном угле - ОНИ опирается на дуги, которые в ДВА раза больше их.
Дуга ˘ВС=˘AВ=2a
проведем прямые (AO1) и (AO)
точки ИХ пересечения с описанной окружностью т.С1 и т.С2
треугольник ОАО1 - равнобедренный , прямая (AC) - биссектриса <C1AC2
значит <C1AC=<C2AC=<a/2 - это вписанные углы
По теореме о вписанном угле - ОНИ опирается на дуги, которые в ДВА раза больше их.
Дуга ˘СС1=˘СС2=a
Прямая (АС2) проходит через центр описанной окружности |AC2| - диаметр
Угол <AOC2 - центральный , развернутый (180 град) -опирается на дугу ˘АС2=180 град.
Дуга ˘АС2 состоит из частей ˘АС2=˘AВ+˘ВС+˘СС2=2a+2a+a=5a=180 , тогда а=180/5=36 град.
<A=<C=<a=36 град
<B=180-<A-<C=180-2*36=108 град
ОТВЕТ углы треугольника 36; 36; 108