Предмет: Геометрия,
автор: vika0513
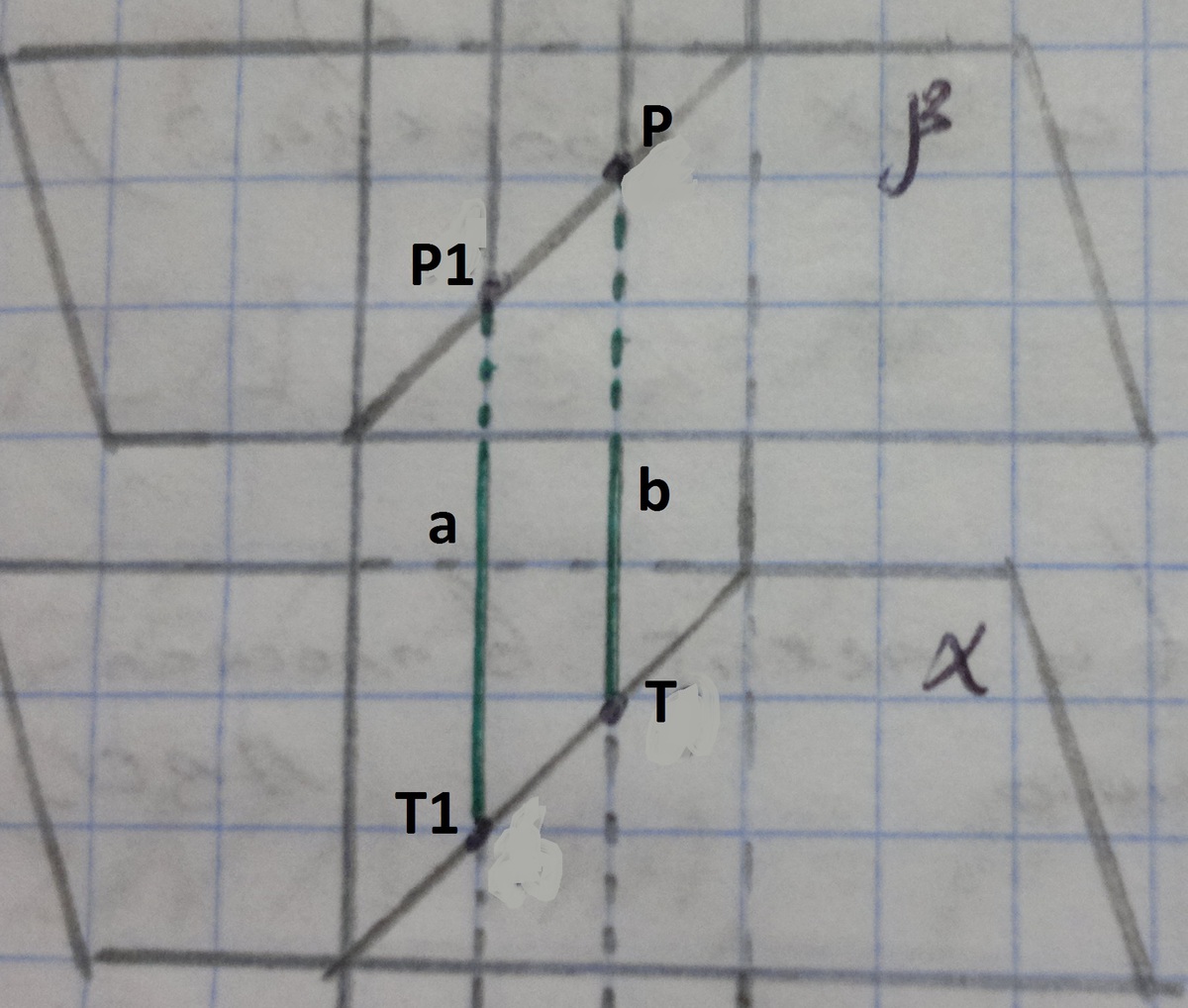
Даны две параллельные прямые и точки Р и Т на одной из
них. Через эти точки проведены параллельные плоскости,
которые пересекают вторую прямую в точках Р1 и Т1
соответственно. Чему равна длина отрезка Р1Т1, если
РТ=6,3дм? Ответ объясните.
С решением плииииз!!!!!!
Ответы
Автор ответа:
0
По свойству параллельных плоскостей: отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
a//b, α//β; T1P1∈a, TP∈b; T1 и T∈α, P1 и P∈β =>
T1P=TP=6,3дм.
Ну либо: Пусть Р1РТТ1 - плоскость ω => ω пересекает α в Т и Т1, β - Р и Р1 => т.к. α//β, то РР1//ТТ1.
РР1//ТТ1, РТ//Р1Т1 (т.к. T1P1∈a, TP∈b, и α//β) => Р1РТТ1 - параллелограмм => TT1=PP1, PT//P1T1 ( по свойству парал-ма) =>
T1P=TP=6,3дм.
a//b, α//β; T1P1∈a, TP∈b; T1 и T∈α, P1 и P∈β =>
T1P=TP=6,3дм.
Ну либо: Пусть Р1РТТ1 - плоскость ω => ω пересекает α в Т и Т1, β - Р и Р1 => т.к. α//β, то РР1//ТТ1.
РР1//ТТ1, РТ//Р1Т1 (т.к. T1P1∈a, TP∈b, и α//β) => Р1РТТ1 - параллелограмм => TT1=PP1, PT//P1T1 ( по свойству парал-ма) =>
T1P=TP=6,3дм.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: samik1517
Предмет: Қазақ тiлi,
автор: Nurimukh
Предмет: Математика,
автор: rymbai27
Предмет: Физика,
автор: varyaXD
Предмет: История,
автор: alinko1O