Question

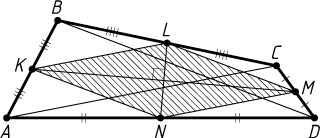
Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, взаимно перпендикулярны и равны 2 и 7. Найти площадь четырехугольника.

Answer 1

Пусть

K,

‍

L,

‍

M

‍и

N

‍середины сторон соответственно

AB,

‍

BC,

‍

CD

‍и

AD

‍выпуклого четырёхугольника

ABCD,

‍

LN = 2,

‍

KM = 7.

‍
Отрезки

KL

‍и

MN —

‍средние линии треугольников

ABC

‍и

ADC,

‍поэтому

KL ‖ AC,

‍

KL = ‍ ‍ 1    ‍ 2  AC,

‍

MN ‖ AC,

‍

MN = ‍ ‍ 1    ‍ 2  AC,

‍значит, четырёхугольник

KLMN —

‍параллелограмм, а так как его диагонали

KM

‍и

LN

‍перпендикулярны, то это — ромб. Площадь ромба равна половине произведения его диагоналей, т. е.

S‍ KLMN  = ‍ ‍ 1    ‍ 2   · 2 · 7 = 7.

‍
Поскольку

KL —

‍средняя линия треугольника

ABC,

‍площадь треугольника

KBL

‍равна четверти площади треугольника

ABC.

‍Аналогично, площадь треугольника

MDN

‍равна четверти площади треугольника

ADC,

‍ поэтому

S‍ △KBL  + S‍ △MDN  = ‍ ‍ 1    ‍ 4  S‍ △ABC  + ‍ ‍ 1    ‍ 4  S‍ △ADC  = ‍ ‍ 1    ‍ 4  (S‍ △ABC  + S‍ △ADC ) = ‍ ‍ 1    ‍ 4  S‍ ABCD .

‍
Аналогично,

S‍ △KAN  + S‍ △MCL  = ‍ ‍ 1    ‍ 4  S‍ ABCD .

‍ Следовательно,

S‍ KLMN  = S‍ ABCD  − S‍ △KBL  − S‍ △MDN  − S‍ △KAN  − S‍ △MCL  =

‍

= S‍ ABCD  − ‍ ‍ 1    ‍ 4  S‍ ABCD  − ‍ ‍ 1    ‍ 4  S‍ ABCD  = S‍ ABCD  − ‍ ‍ 1    ‍ 2  S‍ ABCD  = ‍ ‍ 1    ‍ 2  S‍ ABCD ,

‍

S‍ ABCD  = 2S‍ KLMN  = 2 · 7 = 14.

‍