Предмет: Математика,
автор: SASHA19962011
Ребят, срочно нужна помощь, помогите кто может(((( на второй картинке выделены(зелёным цветом) нужные координаты...
Приложения:


Ответы
Автор ответа:
0
Пусть точка M(x,y) - любая произвольная точка искомой кривой. тогда расстояние от точки A(1,4) до любой точки искомой кривой можно найти по формуле:
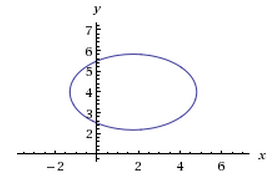
Это уравнение эллипса, О(1,75;4), а=1, b=0,6
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: mari8015
Предмет: Математика,
автор: alexanderkazmin
Предмет: Физика,
автор: Анастасиялогинффф
Предмет: Геометрия,
автор: ленуся66