Question

даны координаты вершин треугольника ABC: A(4;6) В(-4;0), С(-1;-4). Напишите уравнение прямой, содержащей медиану СМ.
Ответ из учебника: 7х-у+3=0. Мне очень нужно решение, пожалуйста.

Answer 1

Определим координаты точки M:

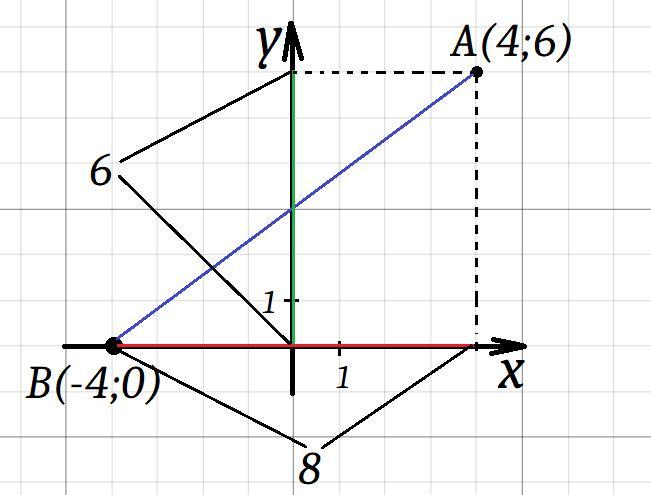
M это середина отрезка AB, отступим от координат конца, в сторону середины, такое число, чтобы при удвоении оно характеризовала длину проекции отрезка на соответствующую ось координат (см. в приложении).

$displaystyle A(4;6),quad B(-4;0)\ AB_x=|4-(-4)|=8;; x=8:2=4\ AB_y=|6-0|=6;; y=6:2=3\ M_x=4-x=4-4=0\ M_y=6-y=6-3=3\ \ boxed{M(0;3)}$

Составим уравнения прямой, проходящей через точки M и C, по формуле: $displaystyle frac{x-x_1}{x_2-x_1} =frac{y-y_1}{y_2-y_1}$ , где (x₁;y₁) и (x₂;y₂) две точки прямой, с различными координатами.

$displaystyle C(-1;-4),quad M(0;3)\ frac{x-(-1)}{0-(-1)} =frac{y-(-4)}{3-(-4)} ;; frac{x+1}{1} =frac{y+4}{7} \ \ 7(x+1)=y+4;; 7x+7-4-y=0\ 7x-y+3=0$

Ответ: 7x-y+3 = 0.

Answer 2

Ответ:

7X - Y +3 = 0

Объяснение:

Находим координаты точки М - медианы СМ:

Xм = (X₁+X₂) / 2 = (4 + (-4)) / 2 = 0

Yм = (Y₁+Y₂)/2 = (6 + 0) / 2 = 3

Уравнение медианы (уравнение прямой, проходящей через точки (Xc; Yc) и (Xм; Yм):

(X - Xм) / (Хс - Хм) = (Y - Yм) / (Yс - Yм)

(X - 0) / (-1 -0) =  (Y -3) / (-4 -3)

X / (-1) =  (Y -3) / (-7)

-7X = -Y+3

7X - Y +3 = 0