Предмет: Алгебра,
автор: MikkiMikki5
Написать уравнение касательной к графику функций f(x)= x^3 - 1 в точке с абсциссой x0 = -1 ; x0 =2
Ответы
Автор ответа:
0
Вот, должно быть правильно.
Приложения:
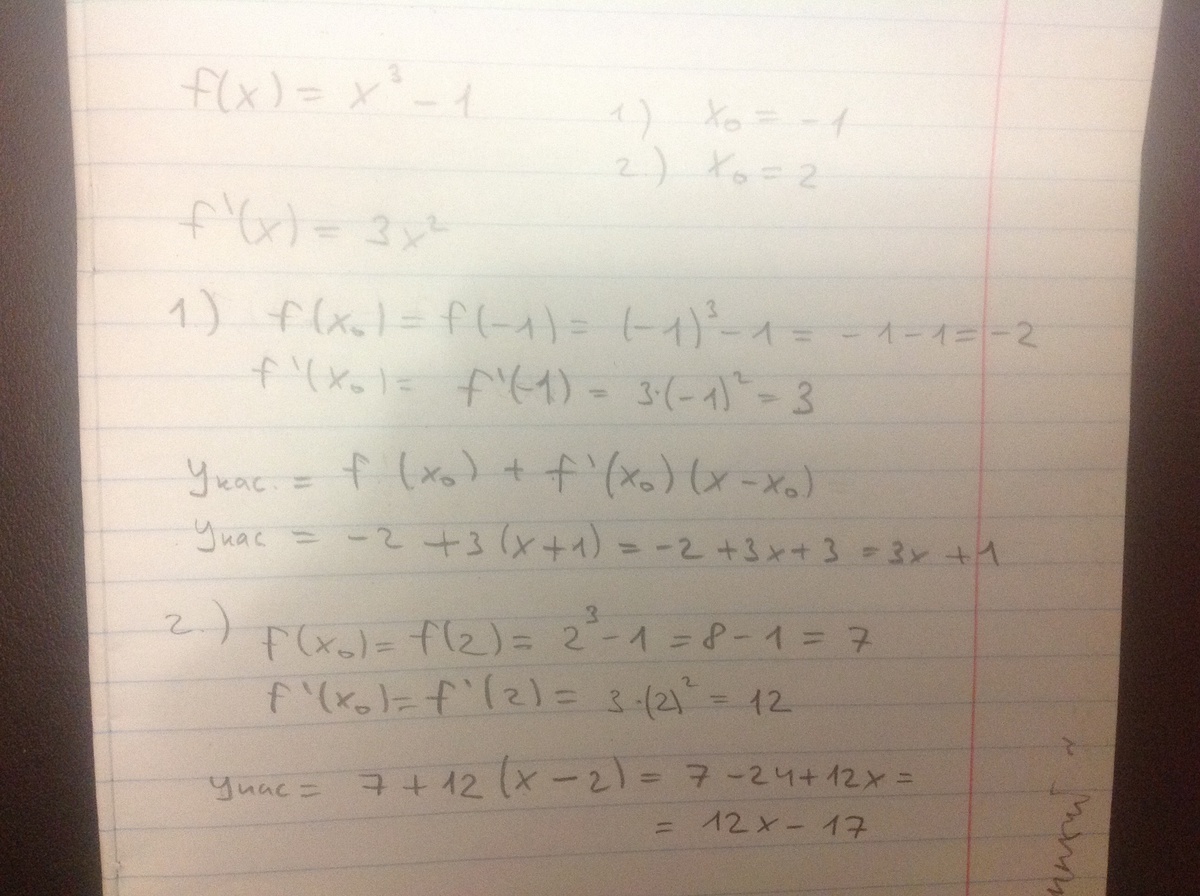
Автор ответа:
0
Запишем уравнения касательной в общем виде:
yk = y0 + y'(x0)(x - x0)
По условию задачи x0 = -1, тогда y0 = -2
Теперь найдем производную:
1) y' = (x3-1)' = 3x2
следовательно:
f'(-1) = 3 (-1)2 = 3
В результате имеем:
yk = y0 + y'(x0)(x - x0)
yk = -2 + 3(x +1)
или
yk = 1+3x
2) Запишем уравнения касательной в общем виде:
yk = y0 + y'(x0)(x - x0)
По условию задачи x0 = 2, тогда y0 = 7
Теперь найдем производную:
y' = (x3-1)' = 3x2
следовательно:
f'(2) = 3 22 = 12
В результате имеем:
yk = y0 + y'(x0)(x - x0)
yk = 7 + 12(x - 2)
или
yk = -17+12x
yk = y0 + y'(x0)(x - x0)
По условию задачи x0 = -1, тогда y0 = -2
Теперь найдем производную:
1) y' = (x3-1)' = 3x2
следовательно:
f'(-1) = 3 (-1)2 = 3
В результате имеем:
yk = y0 + y'(x0)(x - x0)
yk = -2 + 3(x +1)
или
yk = 1+3x
2) Запишем уравнения касательной в общем виде:
yk = y0 + y'(x0)(x - x0)
По условию задачи x0 = 2, тогда y0 = 7
Теперь найдем производную:
y' = (x3-1)' = 3x2
следовательно:
f'(2) = 3 22 = 12
В результате имеем:
yk = y0 + y'(x0)(x - x0)
yk = 7 + 12(x - 2)
или
yk = -17+12x
Приложения:
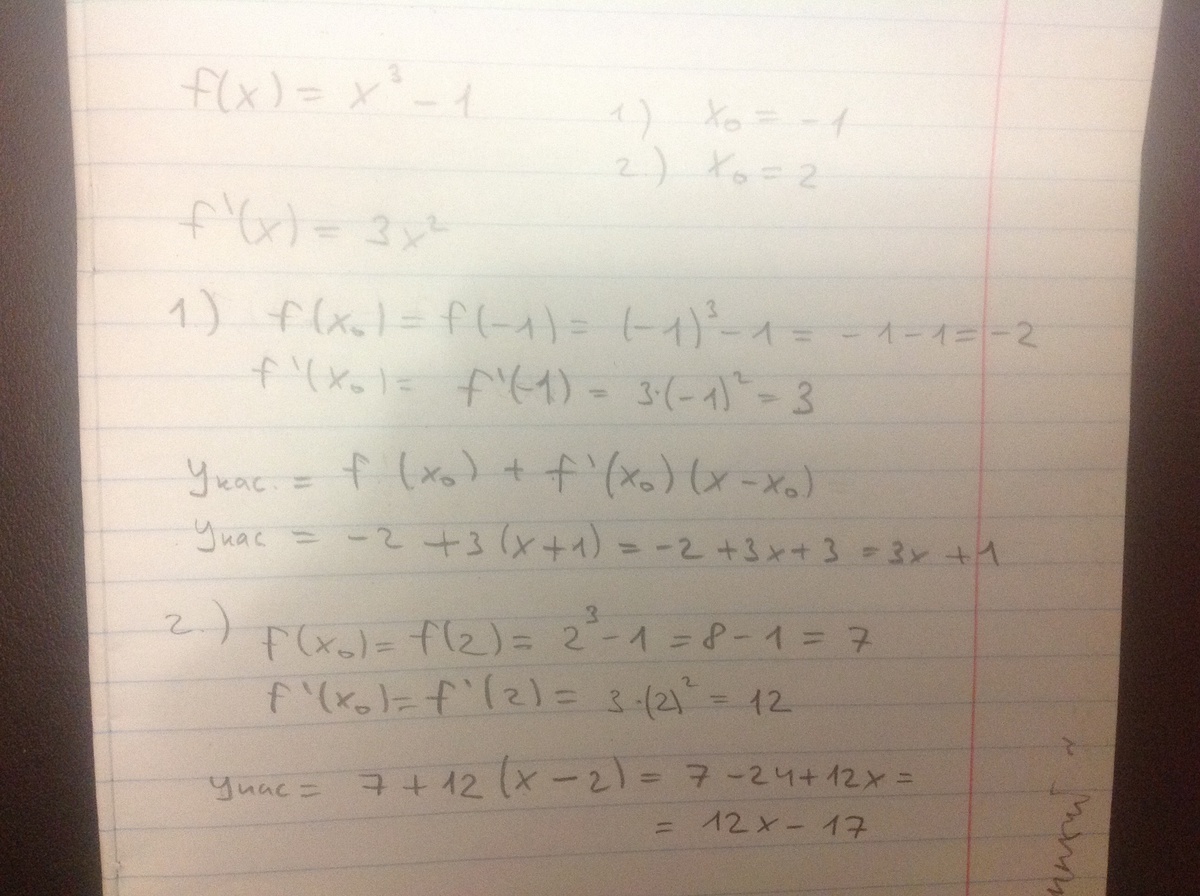
Похожие вопросы
Предмет: Математика,
автор: zaurealimova12
Предмет: Химия,
автор: mokimoki20
Предмет: Алгебра,
автор: ilteslia93
Предмет: Литература,
автор: vlad21092000