Предмет: Геометрия,
автор: irinavlad311
Напишите пожалуйста как решать? Только материал из 7 класса, мне не нужны решения из 10-11 классов
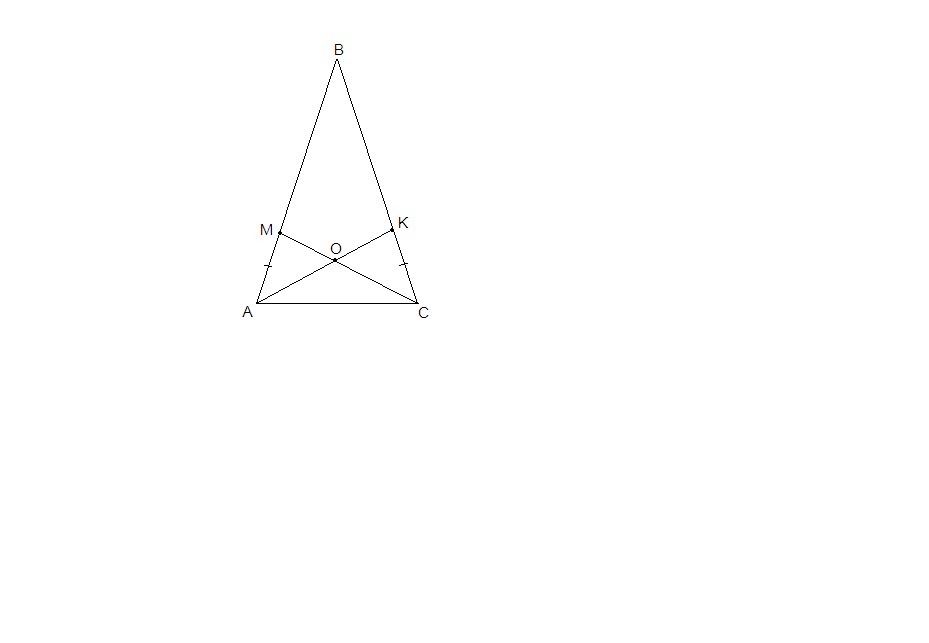
Точки М и К принадлежат соответственно боковым сторонам АВ и ВС равнобедренного треугольника АВС, АМ=СК. Отрезки Ак и СМ пересекаются в точке О. Докажите, что треугольник АОС - равнобедренный.
Заранее спасибо!
Ответы
Автор ответа:
0
∠BAC = ∠BCA как углы при основании равнобедренного треугольника.
АМ = СК по условию.
АС - общая сторона для треугольников АМС и СКА.
Значит, ΔАМС = ΔСКА по двум сторонам и углу между ними.
Из равенства треугольников следует, что ∠АСМ = ∠САК, а это углы при основании треугольника АОС. Следовательно, ΔАОС равнобедренный по признаку.
АМ = СК по условию.
АС - общая сторона для треугольников АМС и СКА.
Значит, ΔАМС = ΔСКА по двум сторонам и углу между ними.
Из равенства треугольников следует, что ∠АСМ = ∠САК, а это углы при основании треугольника АОС. Следовательно, ΔАОС равнобедренный по признаку.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: zavzinm62
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: irinamihailov