Предмет: Математика,
автор: mlgproschool
Установить какая кривая определяется уравнением. Построить её.
16x^2 - 9y^2 - 64x - 54y -161 = 0
Ответы
Автор ответа:
0
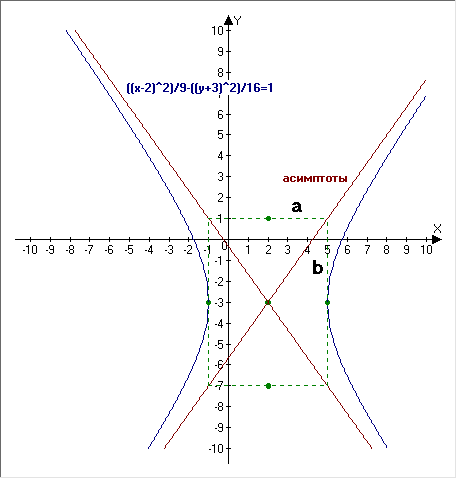
Гипербола с центром в точке (2;-3),a = 3 (действительная полуось); b = 4 (мнимая полуось).
Асимптоты:
Приложения:
Похожие вопросы
Предмет: География,
автор: genises
Предмет: История,
автор: erdanbeket
Предмет: Алгебра,
автор: angelinagordienko055
Предмет: Литература,
автор: Гость1000