Предмет: Алгебра,
автор: neznayka111112
найти предел функции lim ((3*x^2-1)/(3*x^2+5))^(6*x^2+1)
x>бесконечности
Ответы
Автор ответа:
0
Приложения:
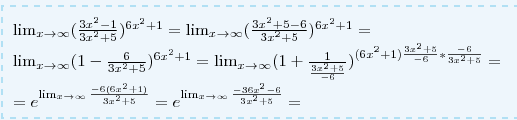
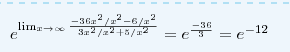
Похожие вопросы
Предмет: Физика,
автор: vladav925
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: suhowerhowat