Предмет: Алгебра,
автор: Аноним
Найти интеграл методом замены переменной
Приложения:
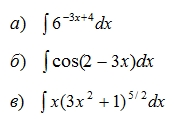
Ответы
Автор ответа:
0
Вроде так,задолбался писать код=/
Похожие вопросы
Предмет: Беларуская мова,
автор: k0nels
Предмет: Оʻzbek tili,
автор: yurain999
Предмет: Музыка,
автор: irenka199712p7ahn2
Предмет: Математика,
автор: илья2