Предмет: Алгебра,
автор: Tatyanka25
Помогите решить логарифмы
Приложения:
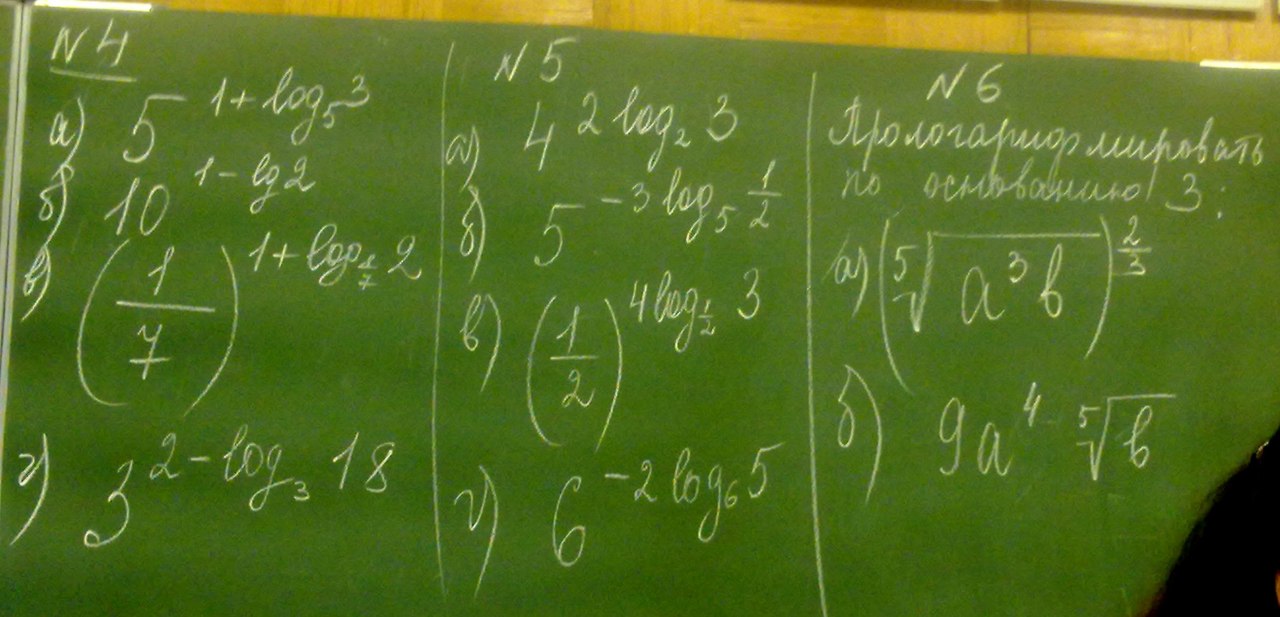
Ответы
Автор ответа:
0
Автор ответа:
0
5^{1+log_5 3}=5cdot5^{log_5 3}=5cdot3=15, \ 10^{1-lg 2}=frac{10}{10^{lg2}}=frac{10}{2}=5, \ (frac{1}{7})^{1+log_{frac{1}{7}} 2}=frac{1}{7}cdot(frac{1}{7})^{log_{frac{1}{7}} 2}=frac{1}{7}cdot2=frac{2}{7}, \ 3^{2-log_3 18}=frac{3^2}{3^{log_3 18}}=frac{9}{18}=frac{1}{9};
Похожие вопросы