Предмет: Математика,
автор: Catadon
3^(2x)-2*3^(x+2)+81>1
где "^" - степень.
Вот этот пример. Я возвела правую часть в квадрат:
Приложения:
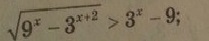
Ответы
Автор ответа:
0
√(9^[x]-3^[x+2]) -3^x+9>0
ОДЗ: 9^[x] -3^[x+2] ≥0
3^[2x]≥3^[x+2]
2x≥x+2
x≥2
Пусть 3^[x] = a
(a²-9a)^[0.5] = a-9
a²-9a=(a-9)²
a(a-9)-(a-9)²=0
(a-9)(a-a+9)=0
9*(a-9)=0
a=9
Возвращаемся к замене
3^[x] = 9
3^[x]=3^[2]
x=2
[2]_____+_____>
Ответ: x ∈ (2;+ω)
ОДЗ: 9^[x] -3^[x+2] ≥0
3^[2x]≥3^[x+2]
2x≥x+2
x≥2
Пусть 3^[x] = a
(a²-9a)^[0.5] = a-9
a²-9a=(a-9)²
a(a-9)-(a-9)²=0
(a-9)(a-a+9)=0
9*(a-9)=0
a=9
Возвращаемся к замене
3^[x] = 9
3^[x]=3^[2]
x=2
[2]_____+_____>
Ответ: x ∈ (2;+ω)
Автор ответа:
0
Преобразуем левую часть неравенства таким образом:
(3^x)²-2×(3^x)×3²+(3²)²>1
Т.е. в левой части получился квадратный двучлен.
Записываем его в виде: (3^x-3²)²>1² или 3^x-9>1 или 3^x>10.
Анализируя полученное неравенство, делаем вывод, что Х>2,...
(3^x)²-2×(3^x)×3²+(3²)²>1
Т.е. в левой части получился квадратный двучлен.
Записываем его в виде: (3^x-3²)²>1² или 3^x-9>1 или 3^x>10.
Анализируя полученное неравенство, делаем вывод, что Х>2,...
Похожие вопросы
Предмет: Химия,
автор: sergeypolumardenov
Предмет: Алгебра,
автор: smirenkoanya
Предмет: Литература,
автор: superdasha446
Предмет: Литература,
автор: lyuba009
Предмет: Информатика,
автор: Gоstь