Question

определите вид четырехугольника который получится если последовательно соединить отрезками середины сторон равнобедренной трапеции, объясните почему

Answer 1

ромб, противоположные углы ровны и стороны равны

Answer 2

Получается Ромб,все стороны которого равны

 

Answer 3

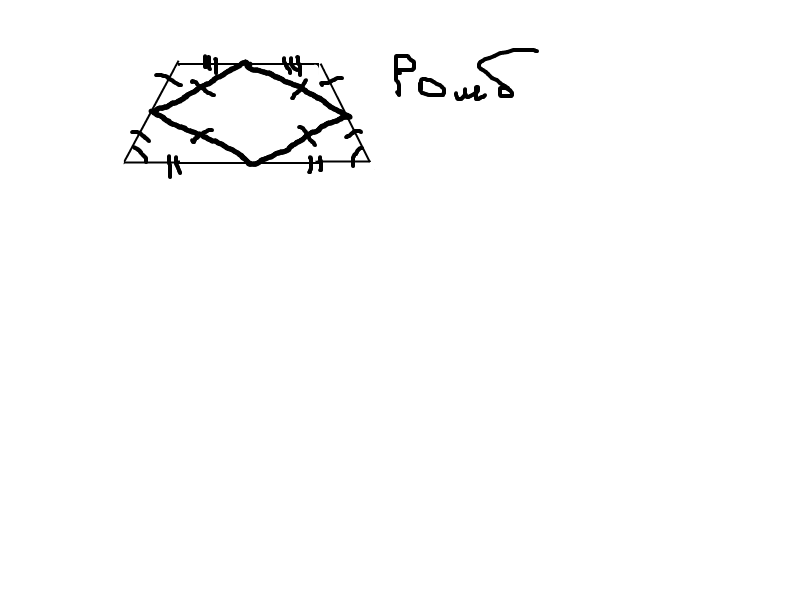
Ответ:

Полученный четырехугольник - ромб.

Объяснение:

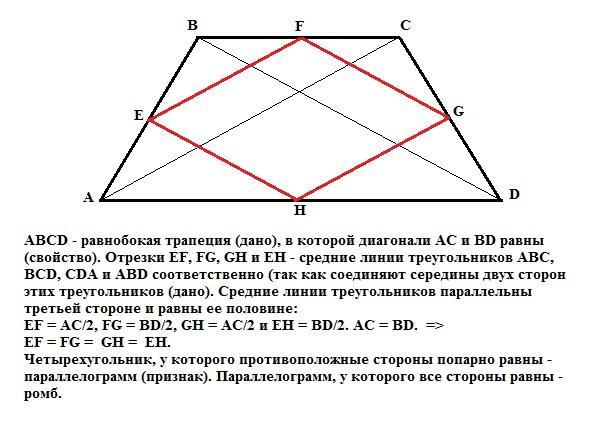
ABCD - равнобокая трапеция (дано), в которой диагонали АС и BD равны (свойство). Отрезки EF, FG, GH и EH - средние линии треугольников АВС, BCD, CDA и ABD соответственно (так как соединяют середины двух сторон этих треугольников (дано). Средние линии треугольников параллельны третьей стороне и равны ее половине:

EF = АС/2, FG = BD/2, GH = AC/2 и EH = BD/2. AC = BD.  =>

EF = FG =  GH =  EH.

Четырехугольник, у которого противоположные стороны попарно равны - параллелограмм (признак). Параллелограмм, у которого все стороны равны - ромб.