Предмет: Математика,
автор: lookina97
ребят объясните как это решить, задание : найдите наибольшее целочисленное решение неравенства.
Приложения:
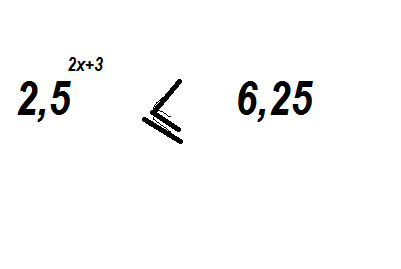
Ответы
Автор ответа:
0
-/-/-/-/-/-/-/-/-/-/-/-/-/--|-/-//-/--|--------------------->
-1 -1/2
-1 - наибольшее целое решение неравенства
Автор ответа:
0
Lookina97, спасибо за лучший )
Автор ответа:
0
Сначала решаете это неравенство, а потом из множества решений находите наибольшее целое число. Теперь решаем неравенство. 6.25=2.25^2, поэтому переписываем это неравенство в виде:
2.5^(2x+3)≤2.5^2.
Основания одинаковы, поэтому данное неравенство напишем следующим образом:
2x+3≤2, решаем данное очень простое неравенство.
2x≤-1
x≤-1/2,
наибольшим целочисленным решением является число -1. Удачи!
2.5^(2x+3)≤2.5^2.
Основания одинаковы, поэтому данное неравенство напишем следующим образом:
2x+3≤2, решаем данное очень простое неравенство.
2x≤-1
x≤-1/2,
наибольшим целочисленным решением является число -1. Удачи!
Похожие вопросы
Предмет: Английский язык,
автор: nastymardasty
Предмет: Математика,
автор: atulepov08
Предмет: Английский язык,
автор: keziknatala5
Предмет: Алгебра,
автор: Аноним