Предмет: Алгебра,
автор: Masimilian
Решить дифференциальное уравнение
y''-3y'+2y=e^x
Ответы
Автор ответа:
0
Это неоднородное дифференциальное уравнение второго порядка.
Сначала нужно найти общее решение соответствующего однородного уравнения. Откинем правую часть и приравняем к нулю.

Теперь необходимо найти какое-либо частное решение неоднородного уравнения.
Ищем частное решение в виде
Выполняем подстановку в наше изначальное диф. ур-ние:

Зная А найдем В, и будем иметь частное решение:

Составляем теперь общее решение неоднородного уравнения:

Сначала нужно найти общее решение соответствующего однородного уравнения. Откинем правую часть и приравняем к нулю.
Теперь необходимо найти какое-либо частное решение неоднородного уравнения.
Ищем частное решение в виде
Выполняем подстановку в наше изначальное диф. ур-ние:
Зная А найдем В, и будем иметь частное решение:
Составляем теперь общее решение неоднородного уравнения:
Приложения:

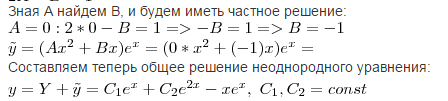
Похожие вопросы
Предмет: Алгебра,
автор: bogdankramor912
Предмет: Биология,
автор: makaron01
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: ilona552
Предмет: Физика,
автор: Iviruss