Предмет: Геометрия,
автор: anastaint
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!! Задачи на доказательства (плииз мне хотяб четверку получить)
Приложения:
Ответы
Автор ответа:
0
Первый уровень
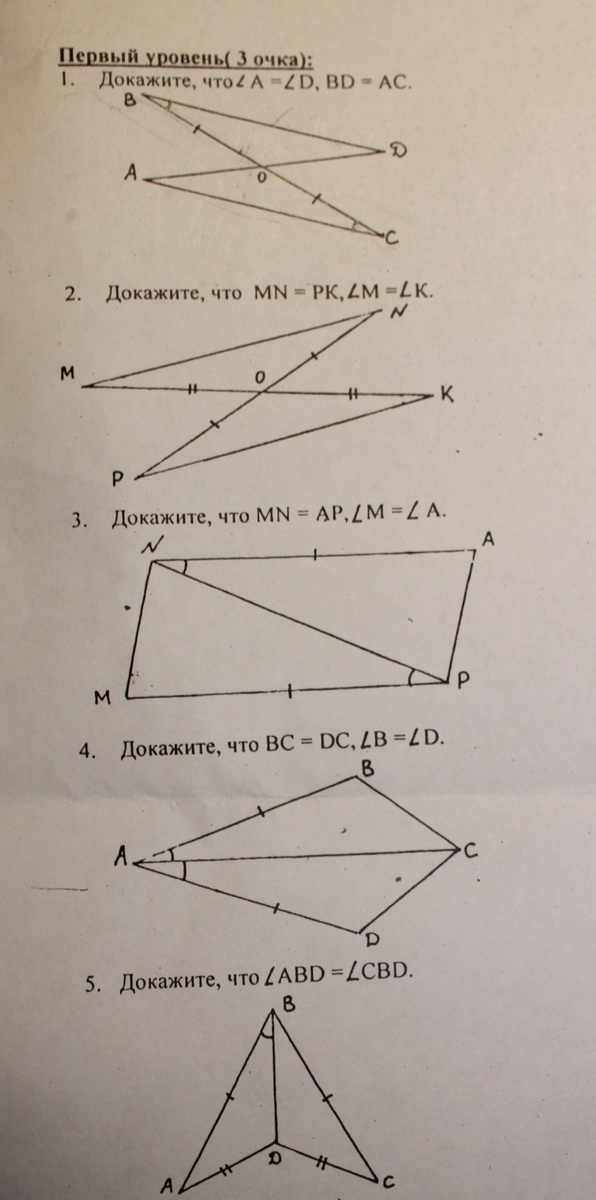
1. Рассмотрим треугольники АОС и DOB. Они равны по второму признаку равенства треуг-ов: сторона и два прилежащих к ней угла одного треуг-ка соответственно равны стороне и двум прилежащим к ней углам другого:
- ВО=СО по условию;
- <B=<С по условию;
- <AOC=<DOB как вертикальные.
У равных треугольников равны соответственные стороны АС и BD, а также углы A и D.
2. Рассмотрим треугольники РОК и NOM. Они равны по первому признаку равенства: две стороны и угол между ними одного треуг-ка соответственно равны двум сторонам и углу между ними другого:
- РО=NO по условию;
- КО=МО по условию;
- <POK=<NOM как вертикальные углы.
У равных треугольников равны соответственные стороны MN и РК и углы М и К.
3. Треугольники ANP и MPN равны по двум сторонам и углу между ними:
- АN=МР по условию;
- NP - общая сторона;
- <ANP=<MPN по условию.
У равных треугольников ANP и MPN равны соответственные стороны MN и АР и углы М и А.
4. Рассмотрим треугольники АВС и ADC. Они равны по двум сторонам и углу между ними:
- AB=AD по условию;
- АС - общая сторона;
- <BAC=<DAC по условию.
У равных треугольников равны соответственные стороны ВС и DC, а также углы B и D.
5. Треугольники ADB и CDB равны по третьему признаку равенства: три стороны одного треугольника соответственно равны трем сторонам другого:
- АВ=СВ по условию;
- AD=CD по условию;
- BD - общая сторона.
У равных треугольников равны соответственные углы ABD и CBD.
Второй уровень:
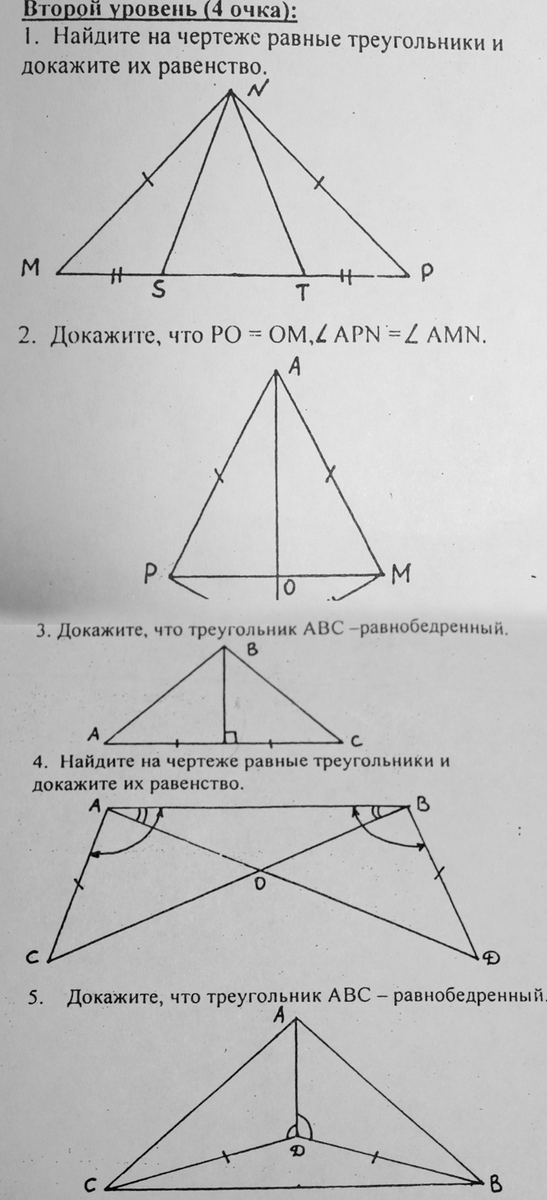
1. Треугольники MNS и PNT равны по двум сторонам и углу между ними:
- MN=PN по условию;
- MS=PT по условию;
- <M=<P, т.к. MNP - равнобедренный треугольник, значит, углы при его основании МР равны.
Треугольники MNT и PNS равны по двум сторонам и углу между ними:
- MN=PN по условию;
- MT=PS (MT=MS+ST, PS=PT+ST, но MS=PT по условию, значит MT=PS);
- углы М и Р равны как углы при основании равнобедренного по условию треугольника MNP.
2. Рисунок виден не полностью
3. Пусть высота будет ВН. Треугольники АНВ и СНВ равны по двум сторонам и углу между ними:
- АН=СН по условию;
- ВН - общая сторона;
- углы АНВ и СНВ прямые.
У равных треугольников равны соответственные стороны АВ и СВ, значит АВС - равнобедренный.
4. Рассмотрим треугольник АОВ. Он равнобедренный, т.к. углы при его основании АВ равны. Значит АО=ВО.
Рассмотрим треугольники САО и DBO. Они равны по двум сторонам и углу между ними:
- СА=DB по условию;
- АО=ВО как доказано выше;
- <CAO=<DBO (<CAO=<CAB-<OAB, <DBO=<DBA-<OBA, но <CAB=<DBA и <OAB=<OBA по условию, значит <CAO=<DBO).
Треугольники CAВ и DBA равны по двум сторонам и углу между ними:
- СА=DB по условию;
- АВ - общая сторона;
- <CAB=<DBA по условию.
5. Треугольники ADC и ADB равны по двум сторонам и углу между ними:
- CD=BD по условию;
- AD - общая сторона;
- <CDA=<BDA по условию.
У равных треугольников равны соответственные стороны АС и АВ. Значит АВС - равнобедренный.
1. Рассмотрим треугольники АОС и DOB. Они равны по второму признаку равенства треуг-ов: сторона и два прилежащих к ней угла одного треуг-ка соответственно равны стороне и двум прилежащим к ней углам другого:
- ВО=СО по условию;
- <B=<С по условию;
- <AOC=<DOB как вертикальные.
У равных треугольников равны соответственные стороны АС и BD, а также углы A и D.
2. Рассмотрим треугольники РОК и NOM. Они равны по первому признаку равенства: две стороны и угол между ними одного треуг-ка соответственно равны двум сторонам и углу между ними другого:
- РО=NO по условию;
- КО=МО по условию;
- <POK=<NOM как вертикальные углы.
У равных треугольников равны соответственные стороны MN и РК и углы М и К.
3. Треугольники ANP и MPN равны по двум сторонам и углу между ними:
- АN=МР по условию;
- NP - общая сторона;
- <ANP=<MPN по условию.
У равных треугольников ANP и MPN равны соответственные стороны MN и АР и углы М и А.
4. Рассмотрим треугольники АВС и ADC. Они равны по двум сторонам и углу между ними:
- AB=AD по условию;
- АС - общая сторона;
- <BAC=<DAC по условию.
У равных треугольников равны соответственные стороны ВС и DC, а также углы B и D.
5. Треугольники ADB и CDB равны по третьему признаку равенства: три стороны одного треугольника соответственно равны трем сторонам другого:
- АВ=СВ по условию;
- AD=CD по условию;
- BD - общая сторона.
У равных треугольников равны соответственные углы ABD и CBD.
Второй уровень:
1. Треугольники MNS и PNT равны по двум сторонам и углу между ними:
- MN=PN по условию;
- MS=PT по условию;
- <M=<P, т.к. MNP - равнобедренный треугольник, значит, углы при его основании МР равны.
Треугольники MNT и PNS равны по двум сторонам и углу между ними:
- MN=PN по условию;
- MT=PS (MT=MS+ST, PS=PT+ST, но MS=PT по условию, значит MT=PS);
- углы М и Р равны как углы при основании равнобедренного по условию треугольника MNP.
2. Рисунок виден не полностью
3. Пусть высота будет ВН. Треугольники АНВ и СНВ равны по двум сторонам и углу между ними:
- АН=СН по условию;
- ВН - общая сторона;
- углы АНВ и СНВ прямые.
У равных треугольников равны соответственные стороны АВ и СВ, значит АВС - равнобедренный.
4. Рассмотрим треугольник АОВ. Он равнобедренный, т.к. углы при его основании АВ равны. Значит АО=ВО.
Рассмотрим треугольники САО и DBO. Они равны по двум сторонам и углу между ними:
- СА=DB по условию;
- АО=ВО как доказано выше;
- <CAO=<DBO (<CAO=<CAB-<OAB, <DBO=<DBA-<OBA, но <CAB=<DBA и <OAB=<OBA по условию, значит <CAO=<DBO).
Треугольники CAВ и DBA равны по двум сторонам и углу между ними:
- СА=DB по условию;
- АВ - общая сторона;
- <CAB=<DBA по условию.
5. Треугольники ADC и ADB равны по двум сторонам и углу между ними:
- CD=BD по условию;
- AD - общая сторона;
- <CDA=<BDA по условию.
У равных треугольников равны соответственные стороны АС и АВ. Значит АВС - равнобедренный.
Похожие вопросы
Предмет: Математика,
автор: rasulovferhad
Предмет: Химия,
автор: anchic198046
Предмет: Математика,
автор: perederijila9
Предмет: Обществознание,
автор: Mashabuuu