Предмет: Алгебра,
автор: ALINshvili
решите плисссссс *((((((
Приложения:
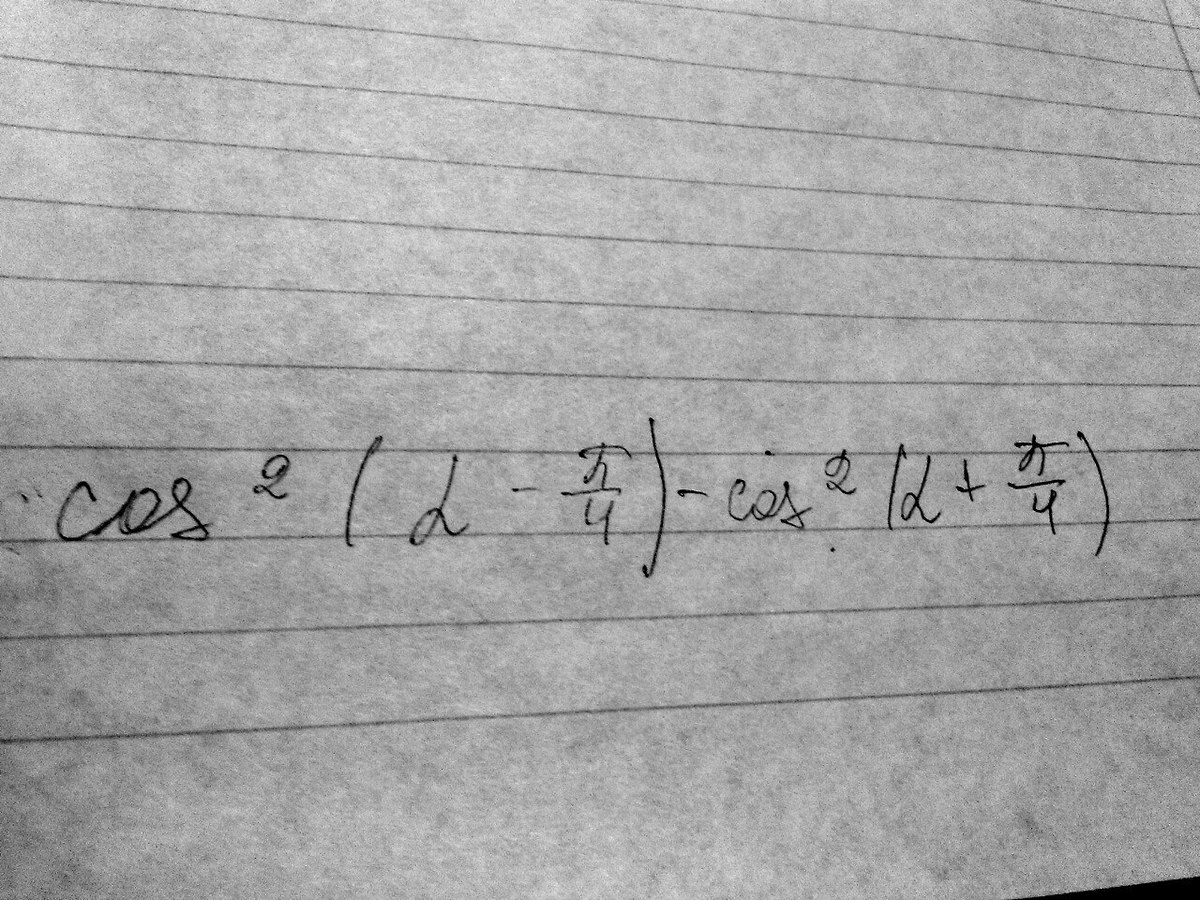
Ответы
Автор ответа:
0
Формула разности квадратов
 (*)
(*)
Далее формулы
соsα-cosβ=-2 sin(α+β)/2 ·sin (α-β)/2
соsα+cosβ=2 cos(α+β)/2 ·cos (α-β)/2
продолжаем
![(*)=-2sin frac{ alpha - frac{ pi }{4}+ alpha + frac{ pi }{4}
}{2}cdot sin frac{ alpha - frac{ pi }{4}- alpha - frac{ pi
}{4} }{2}cdot 2cos frac{ alpha - frac{ pi }{4}+ alpha + frac{
pi }{4} }{2}cdot cosfrac{ alpha - frac{ pi }{4}- alpha - frac{
pi }{4} }{2}= \ =[2singamma cdot cosgamma=sin 2gamma]=-sin2
alpha sin (-frac{ pi }{2})= sin2 alpha (*)=-2sin frac{ alpha - frac{ pi }{4}+ alpha + frac{ pi }{4}
}{2}cdot sin frac{ alpha - frac{ pi }{4}- alpha - frac{ pi
}{4} }{2}cdot 2cos frac{ alpha - frac{ pi }{4}+ alpha + frac{
pi }{4} }{2}cdot cosfrac{ alpha - frac{ pi }{4}- alpha - frac{
pi }{4} }{2}= \ =[2singamma cdot cosgamma=sin 2gamma]=-sin2
alpha sin (-frac{ pi }{2})= sin2 alpha](https://tex.z-dn.net/?f=%28%2A%29%3D-2sin+frac%7B+alpha+-+frac%7B+pi+%7D%7B4%7D%2B+alpha+%2B+frac%7B+pi+%7D%7B4%7D%0A++%7D%7B2%7Dcdot+sin+frac%7B+alpha+-+frac%7B+pi+%7D%7B4%7D-+alpha+-+frac%7B+pi+%0A%7D%7B4%7D++%7D%7B2%7Dcdot++2cos+frac%7B+alpha+-+frac%7B+pi+%7D%7B4%7D%2B+alpha+%2B+frac%7B+%0Api+%7D%7B4%7D++%7D%7B2%7Dcdot+cosfrac%7B+alpha+-+frac%7B+pi+%7D%7B4%7D-+alpha+-+frac%7B+%0Api+%7D%7B4%7D++%7D%7B2%7D%3D+%5C+%3D%5B2singamma+cdot+cosgamma%3Dsin+2gamma%5D%3D-sin2+%0Aalpha+sin+%28-frac%7B+pi+%7D%7B2%7D%29%3D+sin2+alpha+)
Далее формулы
соsα-cosβ=-2 sin(α+β)/2 ·sin (α-β)/2
соsα+cosβ=2 cos(α+β)/2 ·cos (α-β)/2
продолжаем
Похожие вопросы
Предмет: Математика,
автор: guzyaakr07gmailcom
Предмет: Биология,
автор: amanzolovamadina01
Предмет: Қазақ тiлi,
автор: zepro007
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Kriss8383