Question

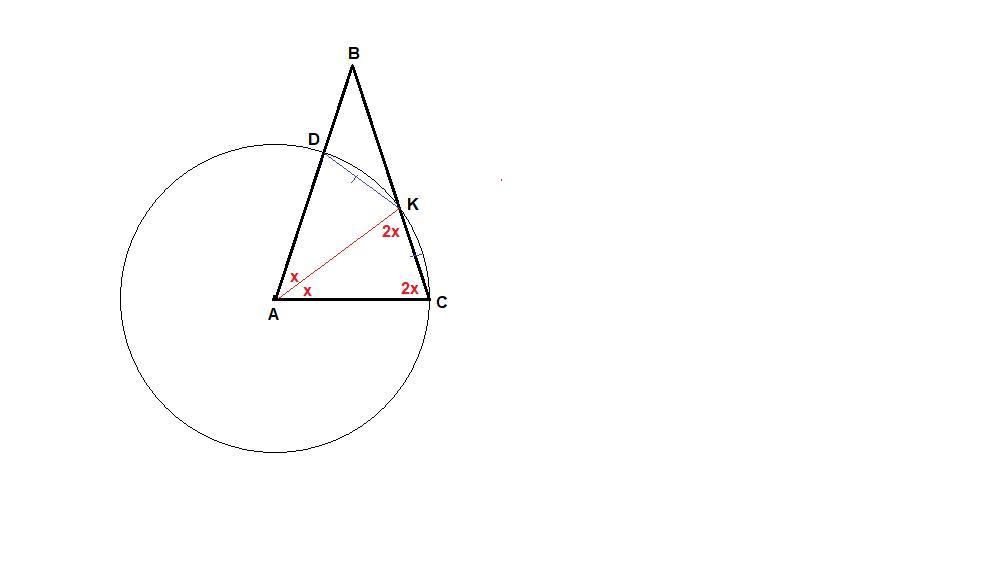
Треугольник ABC равнобедренный, AB= BC.Окружность с центром в точке A радиусом R =AC пересекает сторонуABв точкеD , а сторону BCв точке K,при этом DK=KC .
Найдите углы треугольникаABC.

Answer 1

Ответ:   72°   72°   36°

Объяснение:

AC = AK = AD как радиусы окружности,

DK = KC по условию, значит

ΔDAK = ΔCAK по трем сторонам. Тогда

∠DAK = ∠CAK.

Обозначим ∠DAK = ∠CAK = х. Тогда ∠ВАС = 2х.

∠ВСА = ∠ВАС = 2х как углы при основании равнобедренного треугольника.

ΔАКС так же равнобедренный с основанием KС, значит

∠АКС = ∠АСК = 2х

Для треугольника АСК составим уравнение:

х + 2х + 2х = 180°

5x = 180°

x = 36°

∠BAC = ∠BCA = 36° · 2 = 72°

∠ABC = 180° - (72° · 2) = 180° - 144° = 36°