Question

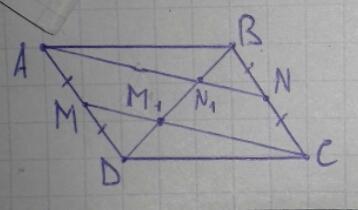
Точки M и N - середины сторон AD и BC параллелограмма ABCD. Докажите, что прямые AN и CM делят диагональ BD на три равные части. Срочно.. Помогите плиз.

Answer 1

AN ∩ BD = N₁

CM ∩ BD = M₁

Если AN и CM делят BD на три равные части, то DM₁ = M₁N₁ = N₁B.

AM=MD и CN=NB по условию. Противоположные стороны параллелограмма равны (AD=BC). Значит, AM=MD=CN=NB.

То есть AM=CN;

AM║NC как отрезки лежащие на противоположных сторонах параллелограмма. Из этого следует, что ANCM - параллелограмм, а значит AN║CM.

В ΔBCM₁ :

NN₁║M₁C, BN=NC ⇒ NN₁ - средняя линия ⇒ BN₁ = N₁M₁.

В ΔDAN₁ :

MM₁║N₁A, DM=MA ⇒ MM₁ - средняя линия ⇒ DM₁ = M₁N₁.

DM₁ = M₁N₁ = N₁B, что и требовалось доказать.