Предмет: Физика,
автор: Lilya21
Помогите, пожалуйста. Задача сложная.Если не знает е решения,проходите мимо.
Груз массой 500 кг находится на плоскости с углом наклона к горизонту альфа = 15°. Чтобы сообщить грузу движение вниз с ускорением 1 м/с^2, необходимо
приложить силу F под углом бетта = 30° к горизонту. Определите величину этой силы, если коэффициент трения = 0,2.
Ответы
Автор ответа:
0
в проекции на оси
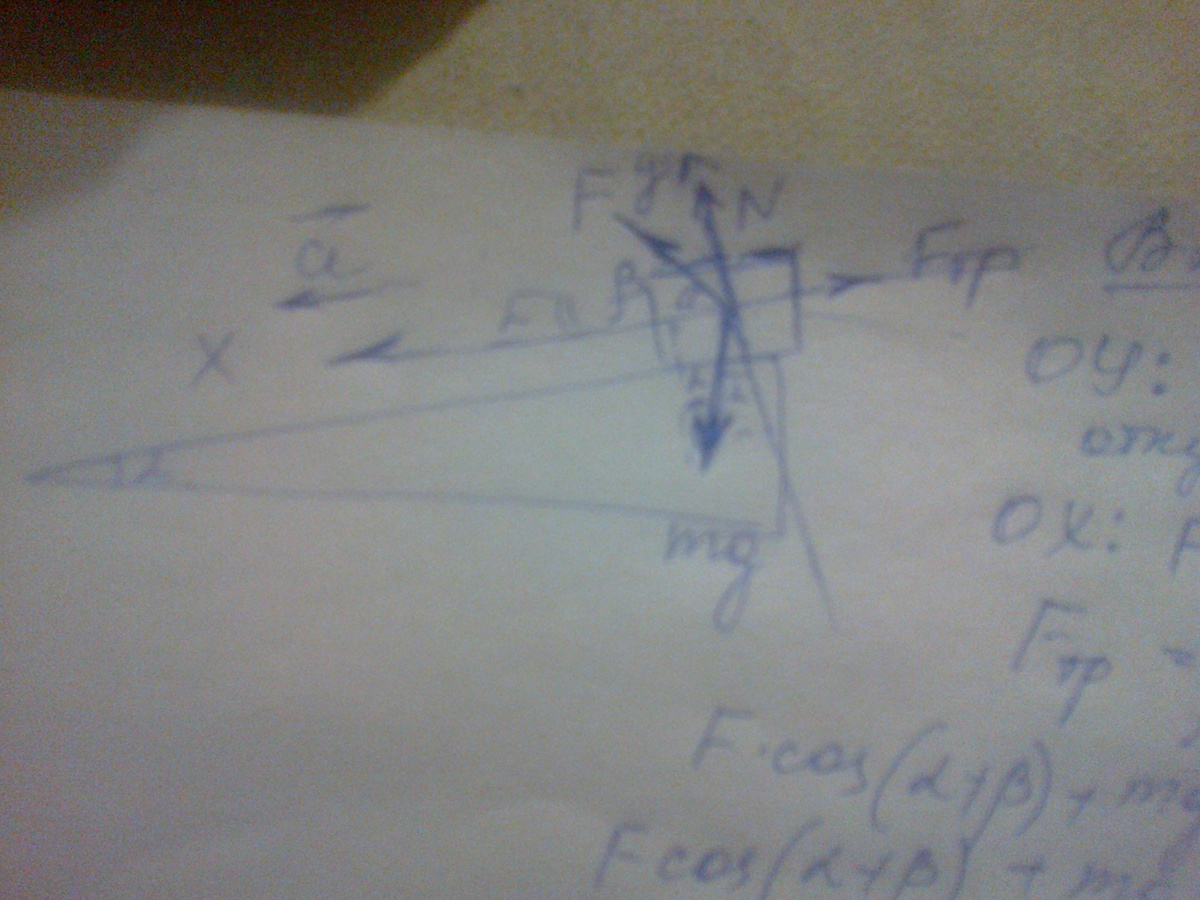
ОУ: Fsin(a+b)-mgcos(a)+N=0 откуда
N=mgcos(a)-Fsin(a+b)
OX: Fcos(a+b)+mgsin(a)-Fтр=ma
Fcos(a+b)+mgsin(a)-мю(mgcos(a)-Fsin(a+b))=ma
F[cos(a+b)+мю*sin(a+b)]=ma-mg(sin(a)-мю*cos(a))
F=[ma-mg(sin(a)-мю*cos(a))]/[cos(a+b)+мю*sin(a+b)]=
=[500*1-500*10(sin15-0,2cos15)]/[cos(15+30)+0,2sin(15+30)]=171.93/0.8485=
=202.6 [Н]=203 [Н]
ОУ: Fsin(a+b)-mgcos(a)+N=0 откуда
N=mgcos(a)-Fsin(a+b)
OX: Fcos(a+b)+mgsin(a)-Fтр=ma
Fcos(a+b)+mgsin(a)-мю(mgcos(a)-Fsin(a+b))=ma
F[cos(a+b)+мю*sin(a+b)]=ma-mg(sin(a)-мю*cos(a))
F=[ma-mg(sin(a)-мю*cos(a))]/[cos(a+b)+мю*sin(a+b)]=
=[500*1-500*10(sin15-0,2cos15)]/[cos(15+30)+0,2sin(15+30)]=171.93/0.8485=
=202.6 [Н]=203 [Н]
Приложения:
Автор ответа:
0
у самого такое бывает
Автор ответа:
0
спасибо за выбор!
Автор ответа:
0
Сила трения:
Fтр = μ(mgCosα - FCos(α+β))
Сила тяги:
Fт = FSin(α+β) + mgSinα
Суммарная сила вдоль склона, вызывающая ускорение a
ma = FSin(α+β) + mgSinα - μ(mgCosα - FCos(α+β))
ma = FSin(α+β) + mgSinα - μmgCosα + μFCos(α+β)
ma - mgSinα + μmgCosα = FSin(α+β) + μFCos(α+β)
m(a - gSinα + μgCosα) = F(Sin(α+β) + μCos(α+β))
F = m(a - gSinα + μgCosα)/(Sin(α+β) + μCos(α+β))
m = 500 кг
α = 15°
β = 30°
g = 10 м с⁻²
μ = 0.2
a = 1 м с⁻²
F = 500*(1 - 2,6 + 1,94)/(0.707 + 0.2*0.707) = 170/0.8484 = 200 Н
Fтр = μ(mgCosα - FCos(α+β))
Сила тяги:
Fт = FSin(α+β) + mgSinα
Суммарная сила вдоль склона, вызывающая ускорение a
ma = FSin(α+β) + mgSinα - μ(mgCosα - FCos(α+β))
ma = FSin(α+β) + mgSinα - μmgCosα + μFCos(α+β)
ma - mgSinα + μmgCosα = FSin(α+β) + μFCos(α+β)
m(a - gSinα + μgCosα) = F(Sin(α+β) + μCos(α+β))
F = m(a - gSinα + μgCosα)/(Sin(α+β) + μCos(α+β))
m = 500 кг
α = 15°
β = 30°
g = 10 м с⁻²
μ = 0.2
a = 1 м с⁻²
F = 500*(1 - 2,6 + 1,94)/(0.707 + 0.2*0.707) = 170/0.8484 = 200 Н
Приложения:

Автор ответа:
0
Ну, если только в арифметике не проврался, конечно. Желательно не сдувать, а проверять - мало ли что...
Похожие вопросы
Предмет: Українська мова,
автор: tanyxa7955
Предмет: История,
автор: pavgalk1n
Предмет: Литература,
автор: katizin54
Предмет: Литература,
автор: ниндзя8585485
Предмет: Математика,
автор: kotiknastya