Предмет: Алгебра,
автор: Богоподобен
Решите уравнения очень срочно
Приложения:
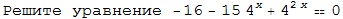
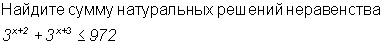
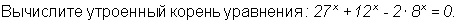
Ответы
Автор ответа:
0
-16-15*4^[x]+4^[2x]=0
Пусть 4^[x]=t (t>0), получаем уравнение
t^2-15t-16=0
Подбераем корни по т . Виета
t1=-1 - не удовлетворяет усл.
t2=16
Возвращаемся к замене
4^[x]=16
4^[x]=4^2
x=2
3^[x+2]+3^[x+3]<=972
9*3^[x]+27^[x]<=972
36*3^[x]<=972
3^[x]<=972:36
3^[x]<=27
3^[x]<=3^3
x<=3
x ∈ (-беск;3]
сумма натуральных чисел: 1+2+3=6
27^[x]+12^[x]-2*8^[x]=0
(27/12)^[x]+1-2*(8/12)^[x]=0
(9/4)^[x]-2*(2/3)^[x]+1=0
(3/2)^[2x]-2*(2/3)^[x]+1=0
Пусть (3/2)^[x]=t, тогда получаем
t^2-2t+1=0
(t-1)^2=0
t=1
Возвращаемся к замене
(3/2)^[x]=1
x=0
Утроенный корень 3x=3*0=0
Пусть 4^[x]=t (t>0), получаем уравнение
t^2-15t-16=0
Подбераем корни по т . Виета
t1=-1 - не удовлетворяет усл.
t2=16
Возвращаемся к замене
4^[x]=16
4^[x]=4^2
x=2
3^[x+2]+3^[x+3]<=972
9*3^[x]+27^[x]<=972
36*3^[x]<=972
3^[x]<=972:36
3^[x]<=27
3^[x]<=3^3
x<=3
x ∈ (-беск;3]
сумма натуральных чисел: 1+2+3=6
27^[x]+12^[x]-2*8^[x]=0
(27/12)^[x]+1-2*(8/12)^[x]=0
(9/4)^[x]-2*(2/3)^[x]+1=0
(3/2)^[2x]-2*(2/3)^[x]+1=0
Пусть (3/2)^[x]=t, тогда получаем
t^2-2t+1=0
(t-1)^2=0
t=1
Возвращаемся к замене
(3/2)^[x]=1
x=0
Утроенный корень 3x=3*0=0
Автор ответа:
0
4^(2x) - 15*4^x - 16 = 0
t = 4^x, t > 0
t^2 - 15t - 16 = 0
t = -1; t = 16 (пользовался теоремой Виета, можете через дискриминант решать)
так как t > 0 следовательно t = 16 (не может быть равен -1)
4^x = 16
4^x = 4^2
x = 2
3^(x+2) + 3^(x+3) <= 972
(3^(x+2)) * (1 + 3) <= 972
4 * 3^(x+2) <= 972
3^(x+2) <= 243
3^(x+2) <= 3^5
x+2 <= 5 (так как функция f = 3^x возрастает)
x <= 3
x = 1; x = 2; x = 3;
Сумма равна 1+2+3=6
27^x + 12^x - 2 * 8^x = 0
3^(3x) + (3^x)*(2^(2x)) - 2 * 2^(3x) = 0 | : 2^(3x), так как 2^(3x) > 0
(3/2)^(3x) + (3/2)^x - 2 = 0
t = (3/2)^x, t > 0
t^3 + t - 2 = 0
Очевидно, что t = 1 это корень,
тогда мы можем разложить многочлен t^3 + t - 2 на множители.
Можно разложить многочлен на множители, поделив многочлен t^3 + t - 2 на многочлен t - 1 или с помощью схемы Горнера (что вам более удобно или знакомо).
(t - 1) * (t^2 - t + 2) = 0
t^2 - t + 2 = 0 или t - 1 =0
t^2 - t + 2 = 0
Дискриминант меньше нуля из этого следует, что t^2 - t + 2 > 0
t - 1 = 0
t = 1
(3/2)^x = 1
x = 0
3*x = 0
Если что-то непонятно, то пишите.
t = 4^x, t > 0
t^2 - 15t - 16 = 0
t = -1; t = 16 (пользовался теоремой Виета, можете через дискриминант решать)
так как t > 0 следовательно t = 16 (не может быть равен -1)
4^x = 16
4^x = 4^2
x = 2
3^(x+2) + 3^(x+3) <= 972
(3^(x+2)) * (1 + 3) <= 972
4 * 3^(x+2) <= 972
3^(x+2) <= 243
3^(x+2) <= 3^5
x+2 <= 5 (так как функция f = 3^x возрастает)
x <= 3
x = 1; x = 2; x = 3;
Сумма равна 1+2+3=6
27^x + 12^x - 2 * 8^x = 0
3^(3x) + (3^x)*(2^(2x)) - 2 * 2^(3x) = 0 | : 2^(3x), так как 2^(3x) > 0
(3/2)^(3x) + (3/2)^x - 2 = 0
t = (3/2)^x, t > 0
t^3 + t - 2 = 0
Очевидно, что t = 1 это корень,
тогда мы можем разложить многочлен t^3 + t - 2 на множители.
Можно разложить многочлен на множители, поделив многочлен t^3 + t - 2 на многочлен t - 1 или с помощью схемы Горнера (что вам более удобно или знакомо).
(t - 1) * (t^2 - t + 2) = 0
t^2 - t + 2 = 0 или t - 1 =0
t^2 - t + 2 = 0
Дискриминант меньше нуля из этого следует, что t^2 - t + 2 > 0
t - 1 = 0
t = 1
(3/2)^x = 1
x = 0
3*x = 0
Если что-то непонятно, то пишите.
Похожие вопросы
Предмет: Другие предметы,
автор: cyanfan
Предмет: Геометрия,
автор: nadagusina111
Предмет: Информатика,
автор: miniakhmetofrustam
Предмет: География,
автор: EvgeshaSav