Предмет: Алгебра,
автор: arbidol32
Решить систему уравнений.
Помогите решить, со всеми графиками, вообщем полное решение.
Приложения:
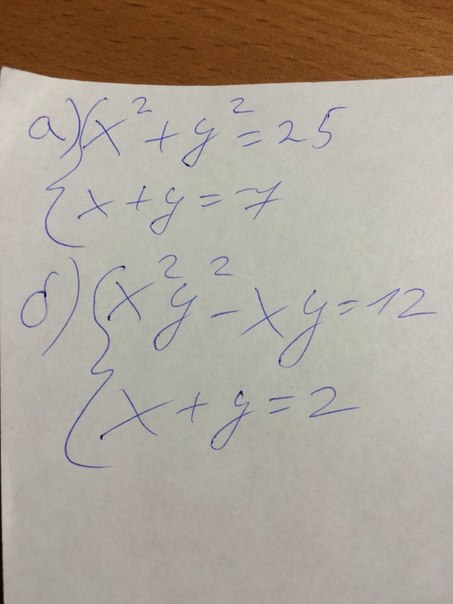
Ответы
Автор ответа:
0
В первой системе - да, графики нужны, потому что там окружность.
А вторую систему вроде и так решить можно: пусть
 , теперь переходим к совокупности двух новых систем:
, теперь переходим к совокупности двух новых систем: 
 , у первой системы нет решений
, у первой системы нет решений
 , сумма коэффициентов равна 0, x=1 и x=-3, но
, сумма коэффициентов равна 0, x=1 и x=-3, но 
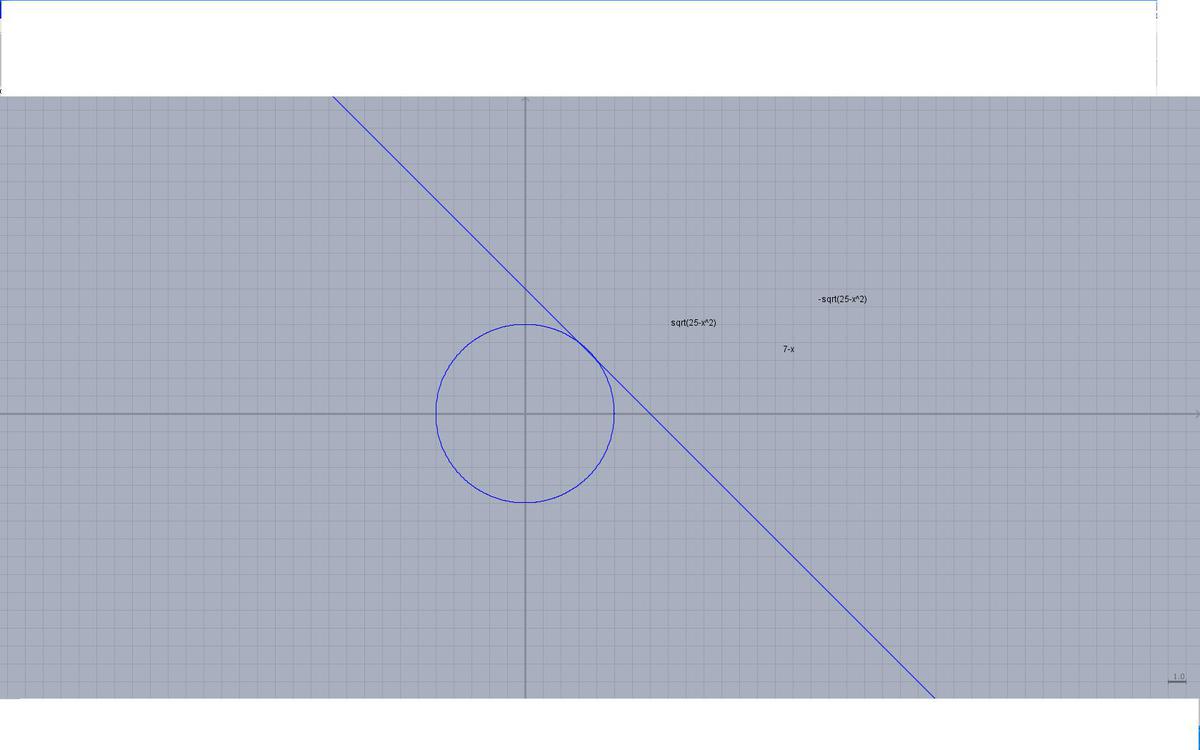
К первой системе графики есть, окружность с центром (0 0), радиус 5.
И прямая y=7-x, т. пересечения (3;4);(4;3)
А вторую систему вроде и так решить можно: пусть
К первой системе графики есть, окружность с центром (0 0), радиус 5.
И прямая y=7-x, т. пересечения (3;4);(4;3)
Приложения:
Автор ответа:
0
А какой будет ответ во 2 примере? Напиши его, пжлс.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: danilgtasanandras
Предмет: Геометрия,
автор: konstantinova250675
Предмет: Алгебра,
автор: sharovaleksei