Предмет: Алгебра,
автор: Scott998
Помогите! Построить график функции  Буду очень благодарен.
Буду очень благодарен.
Ответы
Автор ответа:
0
График не пересекает ось Ox.
Дополнительные точки:
II способ.
Приложения:
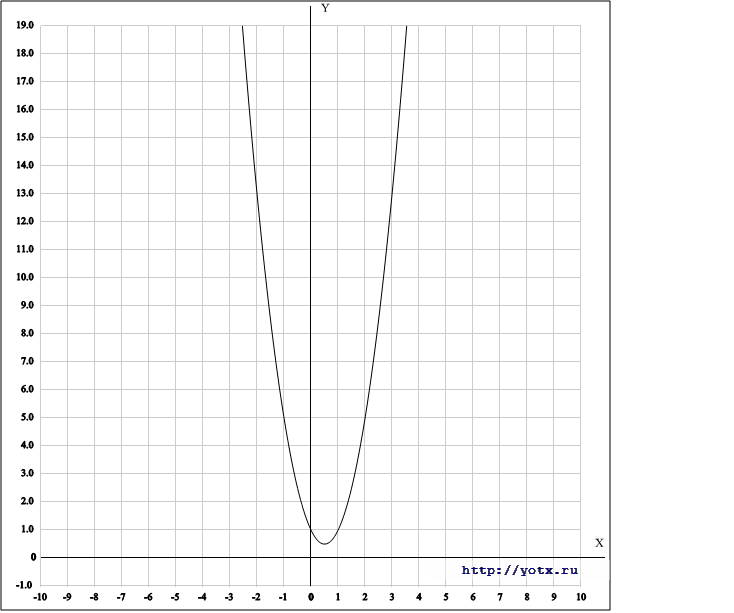
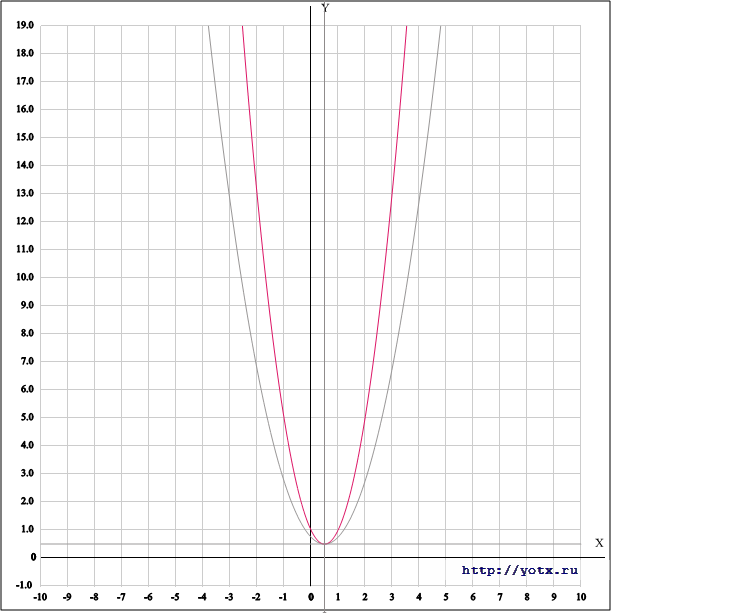
Автор ответа:
0
А можете пожалуйста написать более понятнее? А то не разобрать...
Похожие вопросы
Предмет: Алгебра,
автор: music66684
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: kalpaevemirhan
Предмет: Математика,
автор: sergeync
Предмет: Математика,
автор: mentos4003g