Question

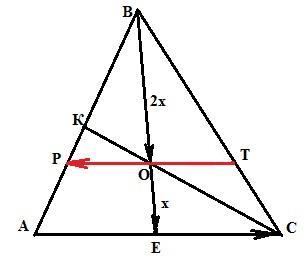
в треугольнике ABC медианы BE и CK пересекаются в точке O. Через точку О проведена прямая, параллельная AC и пересекающая стороны AB и BC в точках P и T. НАЙДИТЕ, если возможно, такое число k, что: 1) TP(вектор) равно kAC (вектор) 2) BO (Вектор) равно kOE( Вектор)

Answer 1

TP=2AC(по правилу о средней линии и основания+PTпроходит через среднюю точку О)

Т.к. точка О-средняя,значит BO=OE.

Answer 2

Ответ:

1). k = -2/3.

2). k =2.

Объяснение:

Медианы треугольника пересекаются в одной точке, которая делит из в отношении 2:1, считая от вершины.

1). Треугольники РВТ и АВС подобны, так как прямая РТ параллельна стороне АС (дано). Коэффициент  подобия треугольников

k = ВО/ВЕ = 2/3 (так как BO/OE=2/1 => ВЕ = 2х+1х = 3х). ТР/АС=2/3.

Так как векторы ТР и АС направлены в разные стороны,

Вектор TP = -(2/3)*АС.  k = -2/3.  

2). ВЕ - медиана. Следовательно, векторы ВО и ОЕ связаны отношением 2:1. Векторы ВО и ОЕ сонаправлены, значит

BO = 2*OE =>  k = 2