Предмет: Алгебра,
автор: mariaslavina
2 вариант, кто сколько сможет
Приложения:
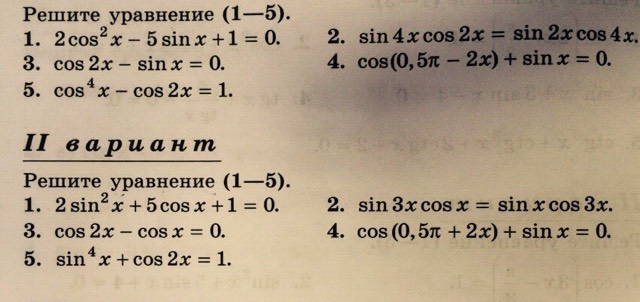
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: ilovenaviundnavi
Предмет: Английский язык,
автор: askarzhasulan813
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: ильтик