Question

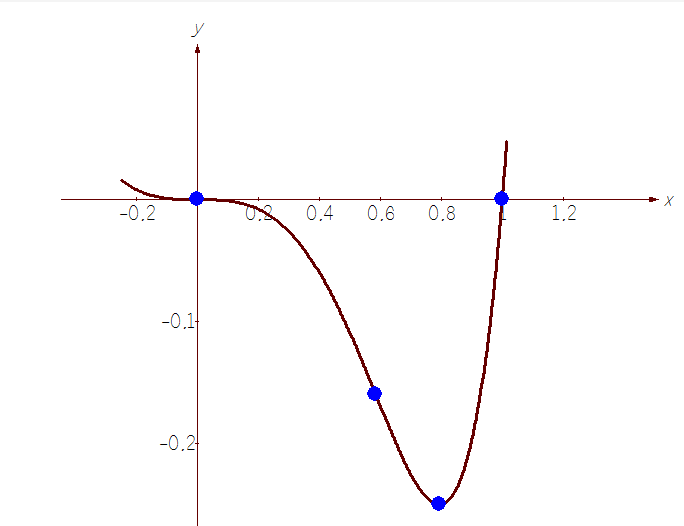
Исследовать функцию с помощью производной и построить график y=x^6-x^3

Answer 1

$y=x^6-x^3$
1. Область определения функции
$D(y)=R$ - множество всех действительных чисел.
2. Исследовать на четность
$y(-x)=(-x)^6-(-x)^3=x^6+x^3$
Итак, функция ни четная ни нечетная.
3. Функция не пертодическая
4. Точки пересечения с осью Ох и Оу
4.1. Точки пересечения с осью Ох
$x^6+x^3=0 \ x^3(x^3+1)=0 \ x_1=0;,,,,,,,x_2=-1$
(0;0), (-1;0) - точки пересечения с осью Ох
4.2. Точки пересечения с осью Оу
$x=0 \ y=0$
(0;0) - точки пересечения с осью Оу.
5. Критические точки, возрастание и убывание функции
5.1$y'=6x^5-3x^2 \ 3x^2(2x^3-1)=0 \ x_1=0 \ x_2= frac{ sqrt[3]{4} }{2}$
Итак, функция возрает на промежутке $( frac{ sqrt[3]{4} }{2} ;+infty)$, убывает - $(-infty;0)$В точке  х = ∛4/2 - функция имеет локальный минимум. а в точке х=0 - локальный максимум
6 Возможные точки перегиба
$y''=30x^4-6x \ 6x(5x^3-1)=0 \ x_1=0 \ x_2= frac{ sqrt[3]{25} }{5}$