Question

Дано изображение куба ABCDA1B1C1D1
а) постройте отрезок, который является пересечением грани DD1CC1 и плоскости α
б) постройте сечение куба плоскостью α
в) вычислите периметр построенного сечения, если известно, что ребро куба равно 6 см и то, что в плоскости α лежат прямая BB1 и точка M - середина D1C1

Answer 1

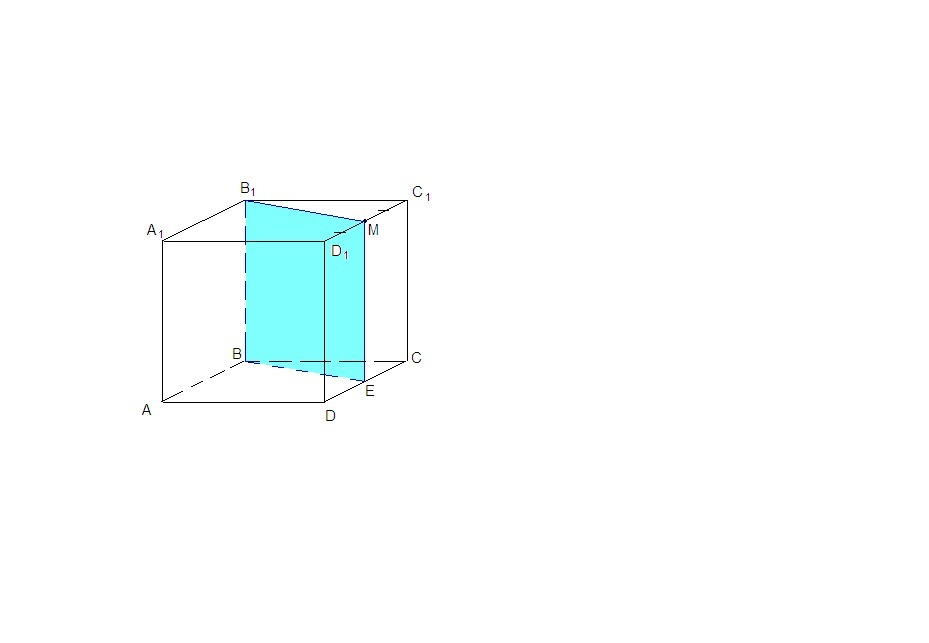
1) СС₁║ВВ₁ как противоположные стороны квадрата, ⇒ ВВ₁║(СС₁D₁),
плоскость α проходит через прямую ВВ₁ параллельную плоскости  боковой грани и пересекает эту плоскость, значит линия пересечения параллельна ВВ₁.
Проведем МЕ║СС₁, а так как СС₁║ВВ₁, то и МЕ║ ВВ₁.
α∩(СС₁D₁) = МЕ.

2) Точки В₁ и М лежат в плоскости одной грани, соединяем их, точки В и Е соединяем, так как они лежат в плоскости одной грани.
ВВ₁МЕ - искомое сечение.

3)  МЕ║СС₁, МС₁║ЕС, ∠С₁СЕ = 90°, значит
МЕСС₁ - прямоугольник. Следовательно
ЕС = МС₁ = C₁D₁/2 = 3 см
МЕ = СС₁ = ВВ₁ = 6 см
ΔЕВС = ΔМВ₁С₁ по двум катетам, значит МВ₁ = ЕВ.

ΔЕСВ: по теореме Пифагора
             ВЕ = √(ВС² + ЕС²) = √(36 + 9) = √45 = 3√5 см
Pвв₁me = (ВВ₁ + ВЕ)·2 = (6 + 3√5)·2 = 6(√5 + 2) см