Предмет: Геометрия,
автор: dastava
Решите задачу плиииииизз!!!!!! Отрезок АВ пересекает плоскость альфа в точке С. Через точки А, В и середину отрезка АВ-точку О-проведены параллельные прямые, пересекающие плоскость альфа в точках А1, В1 и О1 соответственно. Найдите ОО1, если АА1=28 см и ВВ1=21 см.
Ответы
Автор ответа:
0
Соединим А и В₁, В и А₁.
Продолжим ОО₁ в обе стороны до пересечения с АВ₁ в точке О₃ и с ВА₁ в точке О₂
Так как АА₁ || ВВ1₁ || ОО₁, и ВО=ОА, четырехугольник АА₁ВВ₁- трапеция с основаниями АА₁ || ВВ₁, и
О₃О₂- её средняя линия.
Средняя линия трапеции равна полусумме оснований.
О₂О₂=(21+28):2=24,5
ОО₁=О₂О₃-(ОО3+О1О2)
О₁О₂ - средняя линия треугольника ВА₁В₁
ОО₃- средняя линия треугольника АВВ₁
ОО₃=О₁О₂=ВВ₁:2=21:2=10,5
ОО₁=24,5-(10,5+10,5)=3,5 см
Продолжим ОО₁ в обе стороны до пересечения с АВ₁ в точке О₃ и с ВА₁ в точке О₂
Так как АА₁ || ВВ1₁ || ОО₁, и ВО=ОА, четырехугольник АА₁ВВ₁- трапеция с основаниями АА₁ || ВВ₁, и
О₃О₂- её средняя линия.
Средняя линия трапеции равна полусумме оснований.
О₂О₂=(21+28):2=24,5
ОО₁=О₂О₃-(ОО3+О1О2)
О₁О₂ - средняя линия треугольника ВА₁В₁
ОО₃- средняя линия треугольника АВВ₁
ОО₃=О₁О₂=ВВ₁:2=21:2=10,5
ОО₁=24,5-(10,5+10,5)=3,5 см
Приложения:
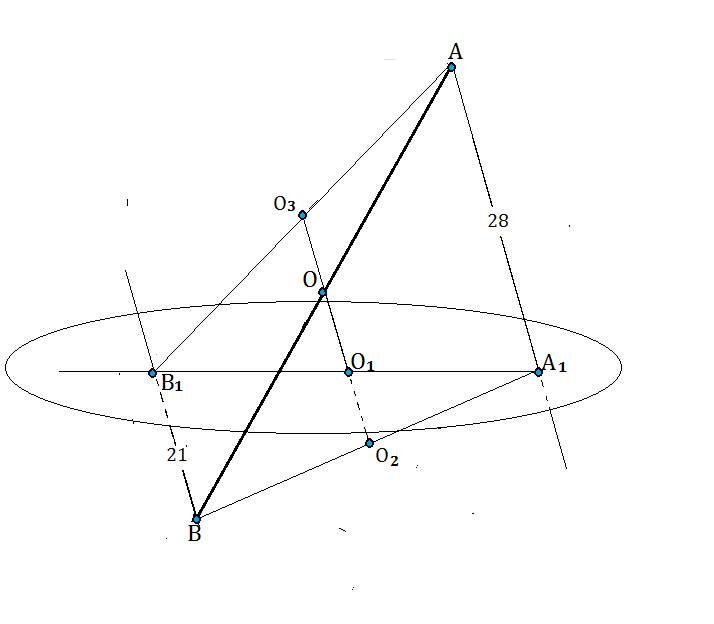
Похожие вопросы
Предмет: Информатика,
автор: pe4enka920
Предмет: Литература,
автор: pologca09
Предмет: Алгебра,
автор: maliisabekova
Предмет: Геометрия,
автор: Маша5555
Предмет: Геометрия,
автор: buffon4ik