Сделать 2 задачи по дномера 959 и 960 с чертежами и все очень поддробно

Ответы
959
a) x^2+y^2=3^2
центр окружности (1;1) радиус r=3
б)
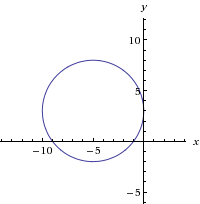
(x+5)^2+(y-3)^2=5^2
центр окружности смещен
по оси ОХ - координата х=-5
по оси ОУ - координата у=3
радиус r=5
в)(x-1)^2+(y+2)^2=2^2
центр окружности смещен
по оси ОХ - координата х=1
по оси ОУ - координата у=-2
радиус r=2
г)
(x-1)^2+y^2=2^2
центр окружности смещен
по оси ОХ - координата х=1
по оси ОУ - координата у=0
радиус r=2
д)
x^2+(y+2)^2=(√2)^2
центр окружности смещен
по оси ОХ - координата х=0
по оси ОУ - координата у=-2
радиус r=√2
960
проверяем по радиусу и длине отрезка
А(3;-4)
B(1;0)
C(0;5)
D(0;0)
E(0;1)
a) x^2+y^2=5^2 r=5
А(3;-4) OA=√(3^2+(-4)^2)=√(9+16)=√25=5 OA=r - т.А лежит на окружности
B(1;0) OB=√(1^2+0^2)=√(1+0)=√1=1 OB<r - т.B лежит внутри окружности
C(0;5) OС=√(0^2+5^2)=√(0+25)=√25=5 OС=r - т.С лежит на окружности
D(0;0) OD=√(0^2+0^2)=√(0+0)=√0=0 OD<r - т.D лежит внутри окружности
E(0;1) OE=√(0^2+1^2)=√(0+1)=√1=1 OE<r - т.E лежит внутри окружности
б) способом подстановки координат точки
(x-1)^2+(y+3)^2=9
А(3;-4) (3-1)^2+((-4)+3)^2 ; 2^2+(-1)^2 =5 < 9 - не лежит на окружности
B(1;0) (1-1)^2+(0+3)^2 ; 0^2+3^2 =9 = 9 - лежит на окружности
C(0;5) (0-1)^2+(5+3)^2 ; (-1)^2+8^2 =65 > 9 - не лежит на окружности
D(0;0) (0-1)^2+(0+3)^2 ; (-1)^2+3^2 =10 > 9 - не лежит на окружности
E(0;1) (0-1)^2+(1+3)^2 ; (-1)^2+4^2 =17 > 9 - не лежит на окружности
в)
способом подстановки координат точки
(x-1/2)^2+y^2=1/4 =0.25
А(3;-4) (x-1/2)^2+y^2 =22.25 >0.25 - не лежит на окружности
B(1;0) (x-1/2)^2+y^2 =0.25 = 0.25 - лежит на окружности
C(0;5) (x-1/2)^2+y^2 =25.25 >0.25- не лежит на окружности
D(0;0) (x-1/2)^2+y^2 =0.25 = 0.25 - лежит на окружности
E(0;1) (x-1/2)^2+y^2 =1.25 >0.25 - не лежит на окружности