Предмет: Геометрия,
автор: onuriya99
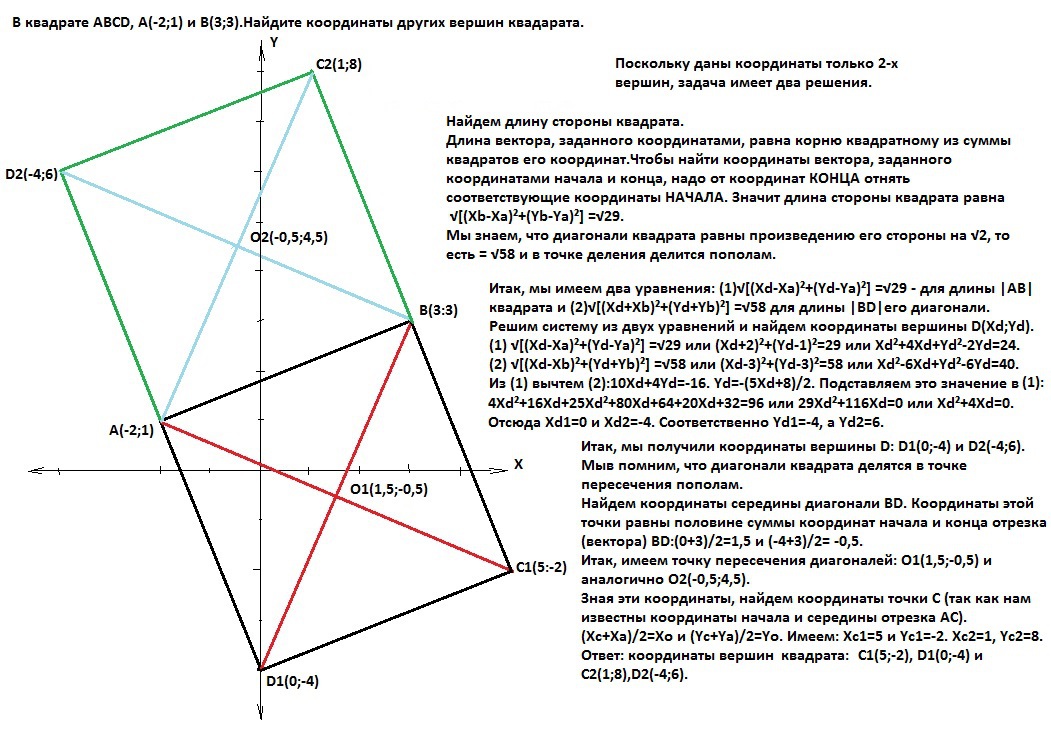
В квадрате ABCD, A(-2;1) и В(3;3).Найдите координаты других вершин квадарата
Ответы
Автор ответа:
0
Поскольку даны координаты только 2-х вершин, задача имеет два решения, так как квадрат может быть построен симметрично относительно стороны АВ..
Найдем длину стороны квадрата.
Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат.Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат КОНЦА отнять соответствующие координаты НАЧАЛА.Значит длина стороны квадрата равна √[(Хb-Xa)²+(Yb-Ya)²] =√29.
Мы знаем, что диагонали квадрата равны произведению его стороны на √2, то есть = √58 и в точке деления делится пополам. Итак, мы имеем два уравнения: (1)√[(Хd-Xa)²+(Yd-Ya)²] =√29 - для длины |АВ| квадрата и (2)√[(Хd+Xb)²+(Yd+Yb)²] =√58 для длины |ВD|его диагонали. Решим систему из двух уравнений и найдем координаты вершины D(Xd;Yd).
(1) √[(Хd-Xa)²+(Yd-Ya)²] =√29 или (Хd+2)²+(Yd-1)²=29 или Хd²+4Хd+Yd²-2Yd=24.
(2) √[(Хd-Xb)²+(Yd+Yb)²] =√58 или (Хd-3)²+(Yd-3)²=58 или Хd²-6Хd+Yd²-6Yd=40.
Из (1) вычтем (2):10Xd+4Yd=-16. Yd=-(5Xd+8)/2.
Подставляем это значение в (1):
4Хd²+16Xd+25Xd²+80Xd+64+20Xd+32=96 или 29Хd²+116Xd=0 или Хd²+4Xd=0. Отсюда Xd1=0 и Xd2=-4. Соответственно Yd1=-4, а Yd2=6.
Итак, мы получили координаты вершины D: D1(0;-4) и D2(-4;6).
Мы помним, что диагонали квадрата делятся в точке пересечения пополам. Найдем координаты середины диагонали BD. Координаты этой точки равны половине суммы координат начала и конца отрезка (вектора) BD: (0+3)/2=1,5 и (-4+3)/2= -0,5.
Итак, имеем точку пересечения диагоналей: О1(1,5;-0,5) и аналогично О2(-0,5;4,5).
Зная эти координаты, найдем координаты точки С (так как нам известны координаты начала и середины отрезка АС.
(Хс+Xa)/2=Xo и (Yc+Ya)/2=Yo. Отсюда имеем: Хс1=5 и Yc1=-2.
Xc2=1, Yc2=8.
Ответ:координаты вершин квадрата: С1(5;-2), D1(0;-4) и C2(1;8),D2(-4;6).
Найдем длину стороны квадрата.
Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат.Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат КОНЦА отнять соответствующие координаты НАЧАЛА.Значит длина стороны квадрата равна √[(Хb-Xa)²+(Yb-Ya)²] =√29.
Мы знаем, что диагонали квадрата равны произведению его стороны на √2, то есть = √58 и в точке деления делится пополам. Итак, мы имеем два уравнения: (1)√[(Хd-Xa)²+(Yd-Ya)²] =√29 - для длины |АВ| квадрата и (2)√[(Хd+Xb)²+(Yd+Yb)²] =√58 для длины |ВD|его диагонали. Решим систему из двух уравнений и найдем координаты вершины D(Xd;Yd).
(1) √[(Хd-Xa)²+(Yd-Ya)²] =√29 или (Хd+2)²+(Yd-1)²=29 или Хd²+4Хd+Yd²-2Yd=24.
(2) √[(Хd-Xb)²+(Yd+Yb)²] =√58 или (Хd-3)²+(Yd-3)²=58 или Хd²-6Хd+Yd²-6Yd=40.
Из (1) вычтем (2):10Xd+4Yd=-16. Yd=-(5Xd+8)/2.
Подставляем это значение в (1):
4Хd²+16Xd+25Xd²+80Xd+64+20Xd+32=96 или 29Хd²+116Xd=0 или Хd²+4Xd=0. Отсюда Xd1=0 и Xd2=-4. Соответственно Yd1=-4, а Yd2=6.
Итак, мы получили координаты вершины D: D1(0;-4) и D2(-4;6).
Мы помним, что диагонали квадрата делятся в точке пересечения пополам. Найдем координаты середины диагонали BD. Координаты этой точки равны половине суммы координат начала и конца отрезка (вектора) BD: (0+3)/2=1,5 и (-4+3)/2= -0,5.
Итак, имеем точку пересечения диагоналей: О1(1,5;-0,5) и аналогично О2(-0,5;4,5).
Зная эти координаты, найдем координаты точки С (так как нам известны координаты начала и середины отрезка АС.
(Хс+Xa)/2=Xo и (Yc+Ya)/2=Yo. Отсюда имеем: Хс1=5 и Yc1=-2.
Xc2=1, Yc2=8.
Ответ:координаты вершин квадрата: С1(5;-2), D1(0;-4) и C2(1;8),D2(-4;6).
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: zhannachan
Предмет: Литература,
автор: alexandryanik
Предмет: Қазақ тiлi,
автор: hafrader
Предмет: Математика,
автор: Sasha1712
Предмет: Алгебра,
автор: evro20051