Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 25 х 40 х 80(см) можно поместить в кузов машины размером 6 х 2 х 2,4(м)
Ответы
Решать эту задачу простым делением объёма кузова на объем коробки нельзя, так как неизвестно, можно ли уложить коробки в кузов так, чтобы нигде не осталось свободного пространства. Нужно предварительно сравнить размеры кузова и размеры коробок.
Наибольшее количество коробок поместится в кузов, если вдоль каждого измерения кузова уложить коробки и не останется пустого пространства. То есть нужно расположить коробки так, чтобы каждая размерность кузова делилась нацело на соответствующий размер прямоугольного параллелепипеда.
Размер коробки 25*40*80 см = 0,25*0,4*0,8 м.
Размер кузова 6*2*2,4 м.
Целое количество коробок размером 0,25 м можно расположить вдоль размеров кузова 6 м и 2 м, но вдоль размера 2,4 м останется пустое пространство, так как
2,4 : 0,25 = 9,6 (9 целых коробок и пустота для части коробки).
Целое количество коробок размером 0,4 м можно расположить вдоль любого размера кузова.
Целое количество коробок размером 0,8 м можно расположить только вдоль размера кузова 2,4 м, так как 6 м и 2 м нацело на 0,8 м не делятся.
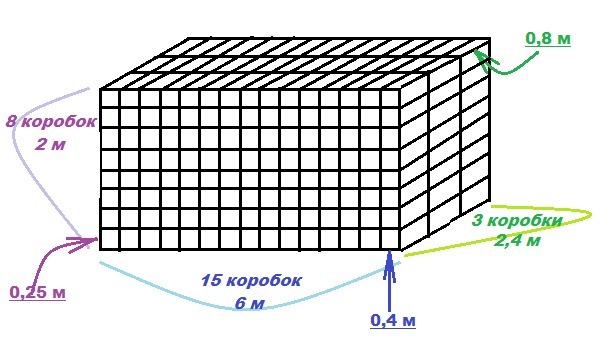
Тогда коробки можно расположить в кузове так:
2 м : 0,25 м = 8 коробок.
6 м : 0,4 м = 15 коробок.
2,4 м : 0,8 м = 3 коробки.
8 * 15 * 3 = 360 коробок заполнят весь объём кузова.
А теперь можно проверить через вычисление объемов
6 * 2 * 2,4 = 28,8 м³ - объём кузова машины
0,25 * 0,4 * 0,8 = 0,08 м³ - объём одного прямоугольного параллелепипеда.
28,8 : 0,08 = 360 коробок.
Ответ: 360 коробок