Предмет: Алгебра,
автор: milkylera
вычислить угол между векторами m и n, если известно, что |m|=1, |n|=2 , и векторы а=2m+6n, b=4m-2n перпендикулярны
Ответы
Автор ответа:
0
Приложения:
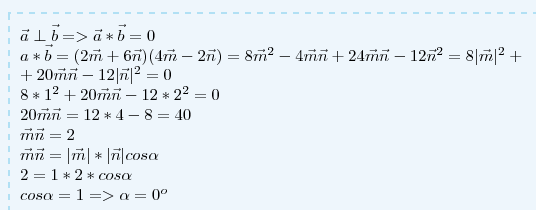
Похожие вопросы
Предмет: География,
автор: dudjfufycy
Предмет: Математика,
автор: khamzinaasema
Предмет: Геометрия,
автор: frosters00
Предмет: Литература,
автор: ВалерияУшакова
Предмет: Математика,
автор: safarovvadim15