Предмет: Геометрия,
автор: АлинаКудрявцева
найдите площадь треугольника, если две его стороны равны 1 и корень из 15, а медиана, проведенная к третьей стороне равна 2
Ответы
Автор ответа:
0
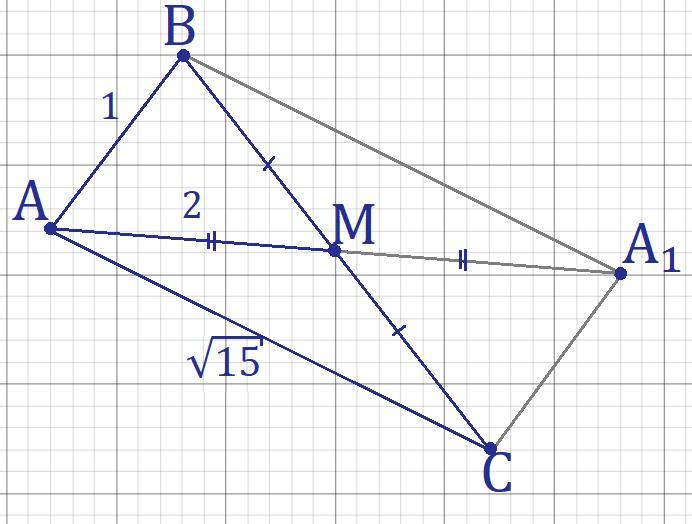
Дано: AB=1; AC=√15; BM=MC; AM=2.
Найти:
Решение:
A₁ ∈ AM; AM=A₁M
ABA₁C - параллелограмм т.к. диагонали делятся точкой пересечения пополам (BM=MC по условию; AM=MA₁ по построению), поэтому A₁C=AB=1.
ΔAA₁C - прямоугольный т.к. выполняется теорема Пифагора:
AA₁² = (2AM)² = (2·2)² = 4² = 16;
AC²+CA₁² = (√15)²+1² = 15+1 = 16;
16 = 16 ⇒ AA₁² = AC²+CA₁².
Поэтому ∠ACA₁ = 90°, он лежит на против гипотенузы AA₁.
ABA₁C - прямоугольник т.к. это параллелограмма с углом в 90° (∠ACA₁=90°), поэтому ∠BAC=90°.
как площадь прямоугольного треугольника (∠BAC=90°).
Ответ:
Приложения:
Автор ответа:
0
Ответ:
решение представлено на фото
Объяснение:
Приложения:

Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: nurdanaeskendir58
Предмет: История,
автор: Ася2015v
Предмет: Литература,
автор: annailiadi127