Question

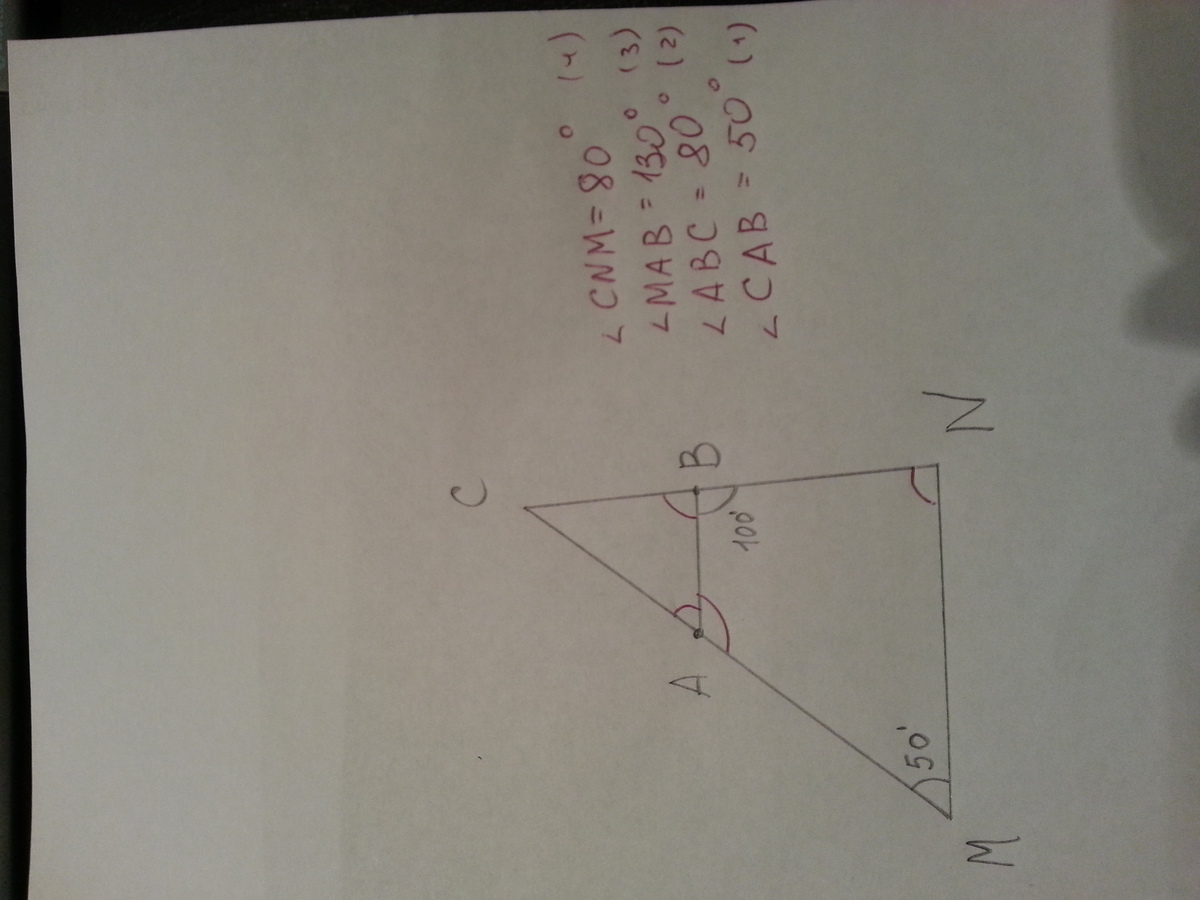
На сторонах МС и NC треугольника MCN взяты соответственно такие точки А и В, что отрезки АВ и MN параллельны. Известно, что угол CMN равен 50 градусов, а угол ABN равен 100 градусов. Найдите величины углов CNM, МАВ, АВС, САВ.

Answer 1

Ну, вот смотри на картинку, а я распишу все по действиям:
1) находим угол САВ: т.к. отрезок АВ параллелен МN, то углы образующиеся при пересечении 2-х параллельных прямых третьей (в нашем случае это MN и АВ параллельные, а МС третья) равны. Значит: угол СМN и угол САВ равны и составляют 50 градусов
2) При определении угла АВС пользуемся свойством прилежащих углов. 180-угол АВN=180-100=80 градусов
3) Точно такой подход и в случае угла МАВ. Углы МАВ и САВ - смежные
180-50=130 градусов
4) Теперь используем свойство углов треугольника.
Сумма углов равна 180 градусов
Узнаем значение угла МСN=180-АВС-СВА=50 градусов
теперь узнаем меру угла CNM=180-CMN-MCN-180-50-50=80 градусов
Все ответы есть на картинке.

Answer 2

Спасибо Вам большое!

Answer 3

Пожалуйста. Главное, чтобы все было понятно в объяснениях