Предмет: Геометрия,
автор: ruslanjf
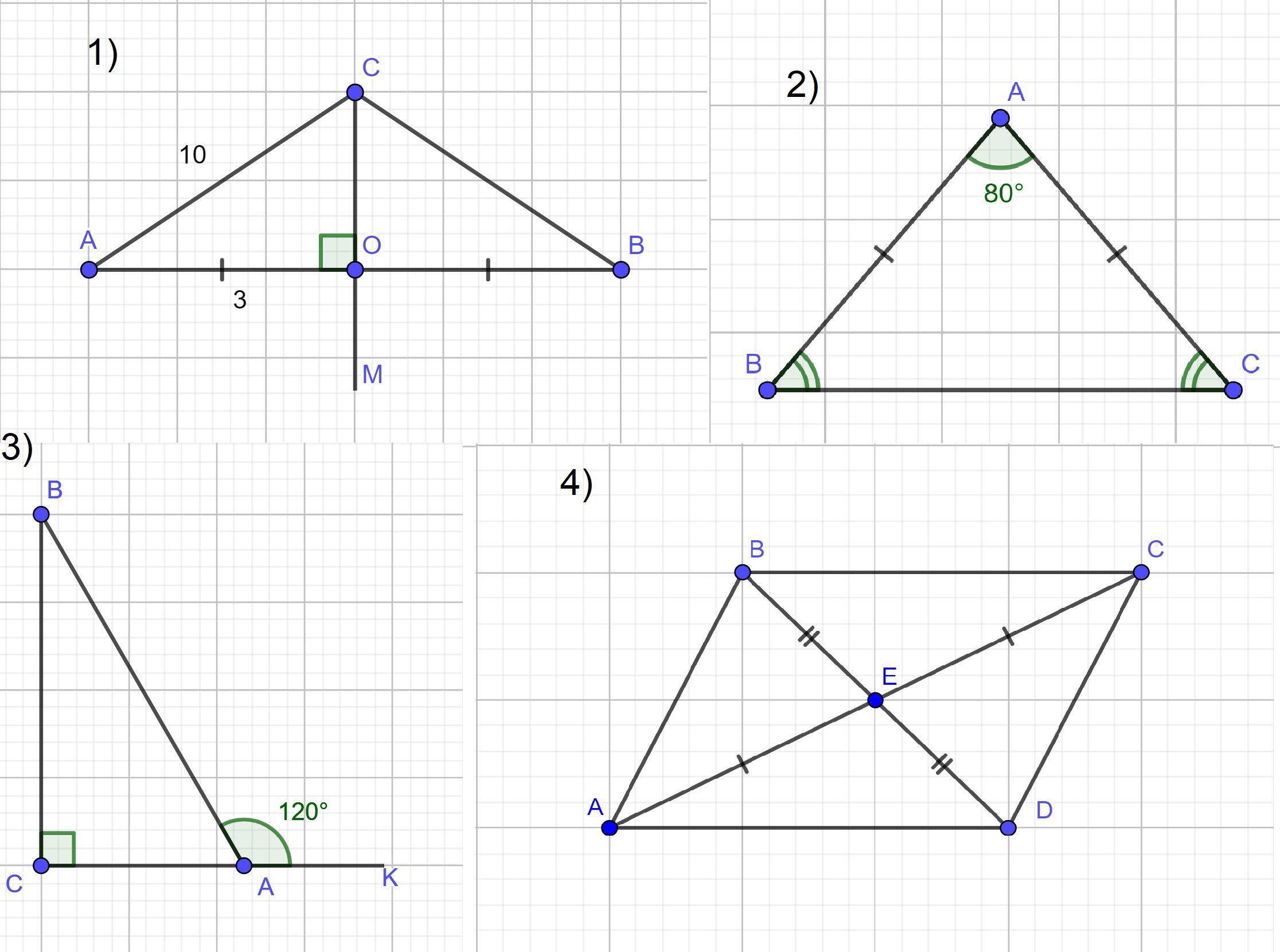
1.Через середину отрезка АВ проведена прямая СМ, пересекающая его в точке О под углом 90°.Известно, что АС=10,АО=3. Найдите ВС.
2.В равнобедренном треугольнике АВС с основанием ВС известно,что угол ВАС равен 80°.Найдите величиу угла АВС.
3.В прямоугольном треугольнике АВС угол С-прямой,внешний угол ВАК=120°, АВ+АС=36.Найдите длину катета АС.
4.В выпуклом четырехугольнике АВСD диагонали пересекаются и точкой пересечения делятся пополам. Найдите меньший угол четырехугольника АВСD,если А:В=2:3
Ответы
Автор ответа:
0
1) ΔAOC = ΔBOC по двум катетам (OC - общий, AO = OB т.к. O - середина AB) ⇒ CB = AC = 10
Ответ: 10
2) В равнобедренном треугольнике углы при основании равны ⇒ ∠ABC = ∠ACB = (180 - 80)/2 = 50°
Ответ: 50°
3) ∠CAB смежный с углом ∠BAK ⇒ ∠CAB = 180 - 120 = 60°
Рассмотрим ΔABC - прямоугольный
∠CAB = 60° ⇒ ∠ABC = 90 - 60 = 30°
Катет, лежащий напротив угла в 30° равен половине гипотенузы: AC = 1/2 AB
Ответ: 12
4) В четырёхугольнике ABCD диагонали пересекаются и точкой пересечения делятся пополам ⇒ ABCD - параллелограмм
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°
Ответ: 72°
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: donchenkovlada935
Предмет: Английский язык,
автор: lazarenkoula432
Предмет: Математика,
автор: Маргорин
Предмет: Литература,
автор: maturemka12345