Предмет: Геометрия,
автор: 888889
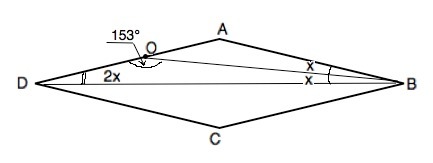
ABCD-ромб.BO-биссектриса угла ABD,угла BOD=153 градуса.Найдите угол C.
Ответы
Автор ответа:
0
Даю подробное решение, т.к. в задачах с таким же условием делается одна и та же ошибка. Если нужно, сократить эту запись не составит труда.
* * *
* * *
ВD - диагональ ромба, является его биссектрисой и делит его углы В и D пополам. ∠АDB=∠ABD
В ∆ АВD биссектриса ВО делит угол АВD пополам.
∠АВО=∠ОВD
Примем угол ОВD=х, тогда угол ОDB=2х
Сумма углов треугольника 180°
В ∆ DOB
∠DOB+∠OBD+∠ODВ=153°+х+2х=153°+3х
153°+3х=180°
3х=27°
х=9°
Угол ВОD внешний для ∆ AOB и равен сумме двух внутренних, не смежных с ним. ⇒
∠А+∠АВО=153°
∠А+9°=153°
∠А=153°-9°=144°
Противоположные углы параллелограмма равны. Ромб - параллелограмм.
Угол С=144°
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Rrvtvgfdddd
Предмет: Алгебра,
автор: 777huligan777
Предмет: Українська мова,
автор: anna09108
Предмет: Алгебра,
автор: kimu
Предмет: Биология,
автор: Златаслава