Question

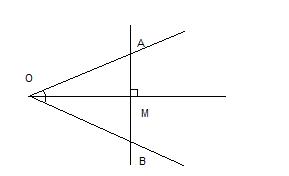
Через точку M, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках A и B. Докажите, что AM=MB.

Answer 1

Имеется два прямоугольных треугольника АМО и ВМО. Эти треугольники равны по одному из признаков равенства прямоугольных треуг-ов: если катет и прилежащий к нему острый угол одного прямоугольного треуг-ка соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. В нашем случае ОМ - общий катет, а углы АОМ и ВОМ равны, поскольку ОМ - биссектриса. У равных треугольников равны и соответственные стороны АМ и ВМ.