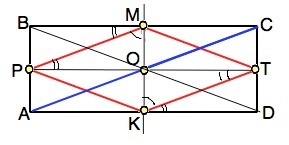
ОЧЕНЬ СРОЧНО!!!!!Ось симметрии прямоугольника ABCD пересекает его стороны BC и AD в точках M и K соответственно.На стороне AB взята точка P,на стороне CD-точка T,причём PM||KT,PM=PK.a)Определите вид выпуклого четырёхугольника PMTK.б)Докажите что расстояние от точки пересечения диагоналей четырёхугольника PMTK до точки C равно PK.
Ответы
МК - ось симметрии, ⇒ все точки АВ и СD находятся от неё на равном расстоянии. ВМ=СМ=АК=DK.
а) Диагонали прямоугольника АС=ВD и точкой пересечения О делятся пополам ( свойство диагоналей прямоугольника).
Отрезки ВМ=АК, а РМ=РК по условию⇒ ∆ МВР = ∆ КАР по катету и гипотенузе. ВР=АР, а ∆ МРК - равнобедренный, МО=ОК. В ∆ АВС. отрезок РМ - средняя линия и параллелен диагонали АС. В ∆ АСD АК=КD, КТ║РМ по условию. Если одна из двух параллельных прямых параллельна третьей, то и вторая ей параллельна. ⇒ КТ║АС – средняя линия ∆ ADC. КТ=АС:2=РМ. Так как КТ - средняя линия ∆ АСD, то, точка Т - середина СD, из чего следует МТ - средняя линия ∆ ВСD. МТ и РК равны половине ВD, следовательно, равны между собой. Стороны четырехугольника КРМТ равны, следовательно, РМТК - ромб.
б) Вершины РМТК - середины сторон прямоугольника, его диагонали РТ и МК пересекаются под прямым углом и делят исходный прямоугольник на четыре равных меньшего размера. Диагонали этих меньших прямоугольников равны. ⇒ РК=АО=ОС, что и требовалось доказать.